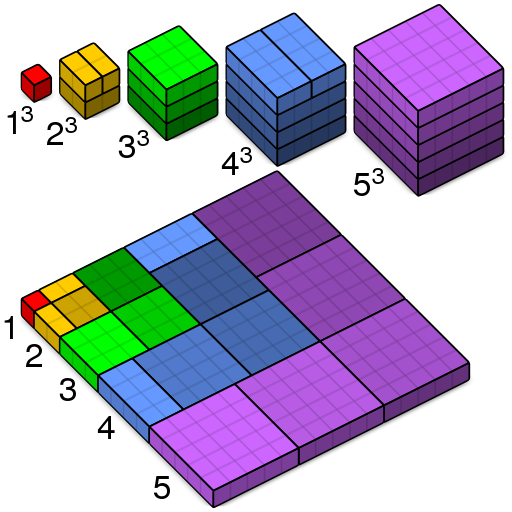
MATLAB’s Loren Shure devised this lovely “proof without words” of Nicomachus’ theorem, that the sum of the first n cubes is the square of the nth triangular number:

R.J. Stroeker of Erasmus University wrote, “Every beginning student of number theory surely must have marveled at [this] miraculous fact.”