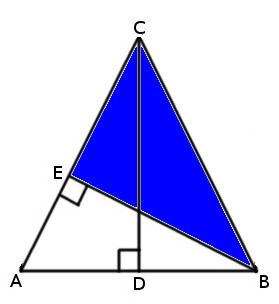
In isosceles triangle ABC, CD = AB and BE is perpendicular to AC. Show that CEB is a 3-4-5 right triangle.
|
SelectClick for Answer |
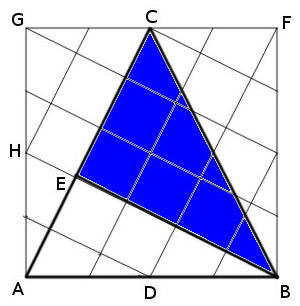
Place triangle ABC into a square and draw the grid shown here, in which each line is parallel to EB or AC and contains a midpoint or quarter point on the side of the square. With CE and BE having lengths 3 and 4, we can determine that hypotenuse CB is of length 5.
“We have therefore shown the nature of this right triangle using a cleverly constructed diagram, and we have avoided lots of tedious computation,” write Alfred S. Posamentier and Ingmar Lehmann in Mathematical Curiosities. “This is an example where we can see how an elegant solution underscores the beauty of mathematics.”
|

