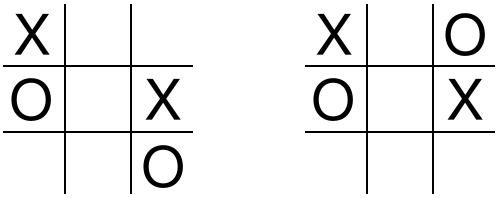This solution is by Clayton W. Dodge of the University of Maine at Orono:
Number the boxes 1-9 from top left to lower right, so that the first column is 1-4-7. Now:
1. The middle box must be empty. If it were marked, say with an X, then the board’s second X would have to be adjacent to it somewhere, and an O must complete that row, column, or diagonal. But now wherever we place the remaining O, the O player can immediately force a win by making a double threat if she has the move. X would be guilty of malpractice for allowing this disaster to come about, and we know she’s an expert player. So it must be X’s turn to move. But now we’ve deduced whose turn it is, and we’ve been told this is impossible. So this whole scenario cannot be the case — the center box must be empty.
2. No two similar marks can appear symmetrically around box 5, since then (if that player has the move) it leads to an immediate win or (if that player doesn’t have the move) we’re violating observation 1 above.
3. The same mark, say X, can’t appear in two adjacent corners, because then an O must appear between them, as well as in another box that will allow O to make two simultaneous threats if she has the move.
4. The same mark, say X, can’t appear in two middle-of-an-edge squares. If Xs appeared in, say, 2 and 8 we’d be violating observation 2. If they appeared in boxes 2 and 4, then one O must go in box 1 (to prevent the double threat) and another in box 6 or 8 to prevent X from winning with box 5. But then O can win with box 9.
5. The same mark, say X, can’t occupy two adjacent squares (say 1 and 2), since then an O must go in box 3 and another box that would allow O to make a double threat if she has the move.
6. Putting all this together, each player has marked one corner and one box opposite to it in the middle of an edge. There are four possibilities:
- If X has played to 1 and 6 and O to 2 and 9, then X can play to 4 and force a win.
- If X has played to 1 and 6 and O to 2 and 7, then X can play to 5 and force a win.
- If X has played to 1 and 6 and O to 4 and either 3 or 9, then expert play will always lead to a draw.
So the envelope must bear one of these two diagrams (or its symmetrical counterpart):
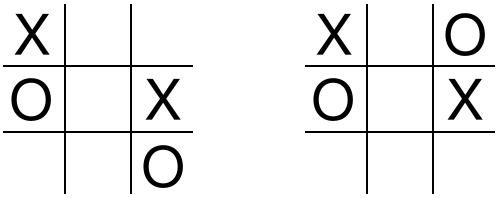
(From Pi Mu Epsilon Journal 5:10 [Spring 1974], 534.)