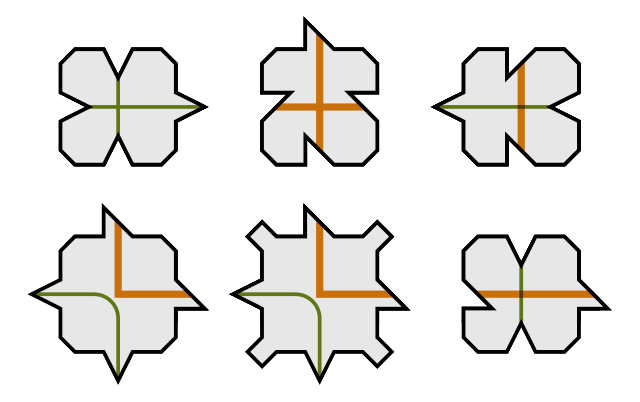
Berkeley mathematician Raphael Robinson discovered this remarkable set of aperiodic tiles in 1978. The six shapes will neatly tile a plane, as shown below, and though the pattern cannot be regular, it reliably produces a hierarchical design: Each small orange square sits at the corner of a larger orange square, which sits at the corner of a still larger one, and so on ad infinitum. This is because subgroups of tiles form “supertiles” with similar properties — see here.

(Thanks, Jacob.)