Dick and Jane are playing a game. Each holds up one or two fingers. If the total number of fingers is odd, then Dick pays Jane that number of dollars. If it’s even, then Jane pays Dick:
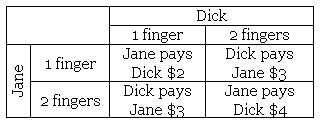
At first blush this looks fair, but in fact it’s distinctly favorable for Jane. Let p be the proportion of times that Jane holds up one finger. Her average winnings when Dick holds up one finger are -2p + 3(1 – p), and her average winnings when he holds up two fingers are 3p – 4(1 – p). If she sets those equal to one another she gets p = 7/12. This means that if she raises one finger with probability 7/12, then on average she’ll win -2(7/12) + 3(5/12) = 1/12 dollar every round, no matter what Dick does. Dick’s best strategy is also to raise one finger 7/12 of the time, but the best this can do is to restrict his loss to 1/12 dollar on average. It’s not a fair game.
