Does the sequence of squares contain an infinite arithmetic subsequence?
Time Out of Joint
In 1582, as the Catholic world prepared to adopt the new Gregorian calendar, German pamphleteers lampooned the strife that attended the change:
The old calendar must be the right one for the animals still use it. The stork flies away according to it, the bear comes out of his hole on the Candlemas day of the old calendar and not of the Pope’s, and the cattle stand up in their stalls to honor the birth of the Lord on the Christmas night of the old and not of the new calendar. They also recognize in this work diabolical wickedness. The Pope was afraid the last day would come too quickly. He has made his new calendar so that Christ will get confused and not know when to come for the last judgment, and the Pope will be able to continue his knavery still longer. May Gott him punish.
“Inanimate objects were not so stubborn.” An Italian walnut tree that had reliably put forth leaves, nuts, and blossoms on the night before Saint John’s day under the old regime dutifully adopted the new calendar and performed its feat on the correct day in 1583. A traveler wrote, “I have today sent a branch, broken off on Saint John’s day, to Herr von Dietrichstein, who no doubt will show it to the Kaiser.”
(Roscoe Lamont, “The Reform of the Julian Calendar,” Popular Astronomy 28:1 [January 1920], 18-32.)
“The Universe and the Philosopher”
The Universe and the Philosopher sat and looked at each other satirically. …
‘You know so many things about me that aren’t true!’ said the Universe to the Philosopher.
‘There are so many things about you that you seem to be unconscious of,’ said the Philosopher to the Universe.
* * *
‘I contain a number of things that I am trying to forget,’ said the Universe.
‘Such as what?’ asked the Philosopher.
‘Such as Philosophers,’ said the Universe.
‘You are wrong,’ said the Philosopher to the Universe, ‘for it is only by working up the most important part of yourself into the form of Philosophers that you get a product capable of understanding you at all.’
‘Suppose,’ said the Universe, ‘that I don’t care about being understood. Suppose that I care more about being?’
‘You are wrong again, then,’ said the Philosopher. ‘For being that is not conscious being can scarcely be called being at all.’
***
‘You Philosophers always were able to get the better of me in argument,’ smiled the Universe, ‘and I think that is one thing that is the matter with you.’
‘If you object to our intellects,’ said the Philosopher, ‘we can only reply that we got them, as well as everything else, from you.’
‘That should make you more humble,’ said the Universe. ‘If I quit letting you have intellect, where would you be then?’
‘Where would you be,’ asked the Philosopher, ‘if you quit letting me have intellect? If I quit thinking you out as you are, and must be, you would cease to exist as you are; for I am a part of you; and if I were to change, your total effect would be changed also.’ … Then the Philosopher reflected a long moment, and, warming to his work, put over this one: ‘The greater part of you, for all I know, exists in my brain anyhow; and if I should cease to think of that part, that part would cease to be.’
* * *
‘You make me feel so helpless, somehow!’ complained the Universe, hypocritically. ‘I beg your pardon for asking you to be humble a moment ago. … I see now, very plainly, that it is I who should be more humble in your presence.’
‘I am glad,’ said the Philosopher, ‘that we have been able to arrive at something like an understanding.’
‘Understanding!’ echoed the Universe. ‘It’s so important, isn’t it?’ … And then: ‘Come! We have argued enough for one day! There is something terribly fatiguing to me about Profound Thought. Can’t we just lie down in the shade the rest of the afternoon and watch the wheels go round?’
‘Watch the wheels go round?’ puzzled the Philosopher.
‘Uh-huh ! … the planets and solar systems, and stuff like that. The nicest thing in life, as I have lived it, is just to lie about and drowse and watch the wheels go round. … I made nearly everything spherical in the beginning so it would roll when I kicked it. I’d rather play than think.’
‘You are a Low Brow!’ said the Philosopher.
‘Uh-huh,’ said the Universe. ‘At times. … I suppose that’s the reason some of the children neglect the old parent these days.’
* * *
And then, after a nap, during which the Philosopher contemplated the Universe with a tinge of superiority, the Universe rumbled sleepily: ‘I know what I am going to do with this Intellect Stuff. I’m going to take it away from you Philosophers and give it to fish or trees or something of that sort!’
‘How frightfully grotesque!’ said the Philosopher, turning pale.
‘Or to giraffes,’ continued the Universe. ‘Giraffes are naturally dignified. And they aren’t meddlesome. I’d like to see a whole thousand of giraffes walking along in a row, with their heads in the air, thinking, thinking, thinking … with tail coats and horn-rimmed goggles.’
* * *
‘You are absurd!’ cried the Philosopher.
‘Uh-huh,’ said the Universe. And reaching over, the Universe picked up the Philosopher, not ungently, by the scruff of the neck, tossed him into the air, caught him tenderly as he came down, spun him around, and set him right side up on the ground.
‘You,’ said the Universe, grinning at the breathless Philosopher pleasantly, ‘are sort of funny yourself, sometimes!’
Performance Review
The index to David Lloyd George’s 1938 War Memoirs sums up his feelings about Field Marshal Douglas Haig:
his refusal to face unpleasant facts
his limited vision
Germans accustomed to his heavy-footed movements
his stubborn mind transfixed on Somme
his misconceptions concerning morale of German army
obsessed with Passchendaele and optimistic as to military outlook
none of his essential conditions for success prevail at Passchendaele
misrepresents French attitude
his plans strongly condemned by Foch
misleads Cabinet about Italian Front
prefers to gamble his hopes on men’s lives than to admit an error
completely ignorant of state of ground at Passchendaele
fails to appreciate the value of tanks
not anxious for success on Italian Front
a mere name to men in the trenches
narrowness of his outlook
incapable of changing his plans
his judgement on general situation warped by his immediate interests
his fanciful estimates of man-power
jealous of Foch
does not expect big German attack in 1918
distributes his reserves very unwisely
his conduct towards Fifth Army not strictly honourable
his unwise staff appointments
his defeatist memorandum of 25/3/18
unfairly removes Gough from command of Fifth Army
his complaints as to lack of men unjustified
does not envisage Americans being of use in 1918
stubbornness
unreliability of his judgments
launches successful attack of 8/8/18 […] but fails to follow it up
his censorious criticism of his associates
his attempt to shirk blame for March, 1918, defeat
only took part in one battle during War
Also: “unequal to his task”, “industrious but uninspired”, “did not inspire his men”, “entirely dependent on others for essential information”, “the two documents that prove his incapacity”, “unselfish but self-centred”, “his inability to judge men”, “liked his associates to be silent and gentlemanly”, “his contempt for Foch”, “his intrigues against Lord French and Kitchener”, “his failure at Loos”, “his ingenuity in shifting blame to other shoulders than his own”, “his shabby treatment of Gough”, and “his conspiracy to destroy General Reserve”. He found in Haig’s diaries “a sustained egoism which is almost a disease.”
Proof Without Words
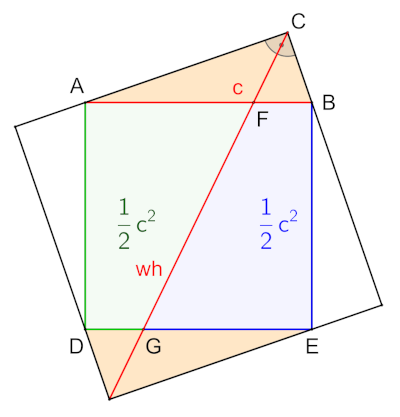
In any right triangle, the angle bisector of the right angle divides the square on the hypotenuse into two congruent trapezoids.
Words and Numbers
fIVe + sIX + seVen
5 + 6 + 7 = 18
IV + IX + V = 18
These are the only three consecutive numbers whose sum equals that of the Roman numerals embedded in their names.
Burattini’s Dragon
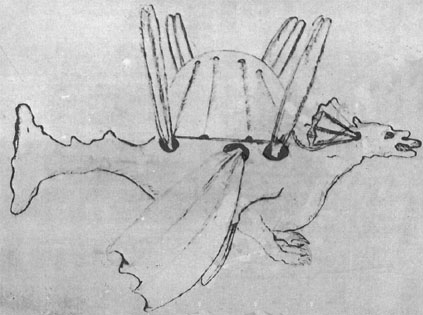
In 1647, Venetian inventor Tito Livio Burattini built a flying machine that could carry a cat. Reportedly the vessel had four pairs of wings and was driven by cords pulled by hand; it “remained airborne as long as a man kept the feathers and wheels in motion by the way of a string.” One observer wrote, “if the cat had the understanding to do that — its strength would be sufficient for this — it would keep itself in the air.”
This 4-foot “Dragon Volant” was only a prototype; Burattini hoped to produce a finished version that could carry a man. By May 1648 he’d brought out an improved model, and German polymath Johann Joachim Becher even mentions a report that the aircraft eventually rose into the air with three people aboard, including the inventor, who “wanted to fly from Warsaw to Constantinople inside 12 hours.” But “as there were always some shortcomings, perfection was never achieved,” and it appears the project ended there.
(Jerzy B. Cynk, Polish Aircraft, 1893-1939, 1971.)
Falling Currency
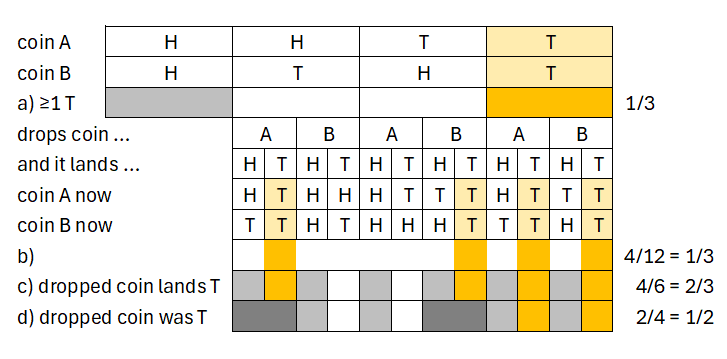
A problem from the October 1964 issue of Eureka, the journal of the Cambridge University Mathematical Society:
My friend tosses two coins and covers them with his hand. ‘Is there at least one “tail”?’ I ask. He affirms this (a).
Just then he accidentally knocks one of them to the floor (b). On finding the dropped coin under the table, we discover it to be a ‘tail’ (c).
‘That is all right,’ he says, ‘because it was a “tail” to start with.’ (d).
At each point (a), (b), (c) and (d) of this episode I calculated what, to the best of my knowledge, was the probability that both coins showed ‘tails’ at the time. What were these probabilities?
Modern Times

The sea urchin Coelopleurus exquisitus was discovered on eBay. Marine biologist Simon Coppard was directed to a listing on the site in 2004 and realized that the species had not previously been described. When it was properly named and introduced in Zootaxa two years later, the value of specimens on eBay shot up from $8 to $138.
In 2008 a fossilized aphid on eBay was similarly found to be unidentified. Eventually it was named Mindarus harringtoni, after the buyer.
Unquote
“A conference is a gathering of important people who singly can do nothing, but together can decide that nothing can be done.” — Fred Allen