Search Results for: lee sallows
Sure Enough
From Lee Sallows, “A novel geometric proof that 16 is a square number.” :)
(Thanks, Lee!)
Inventory
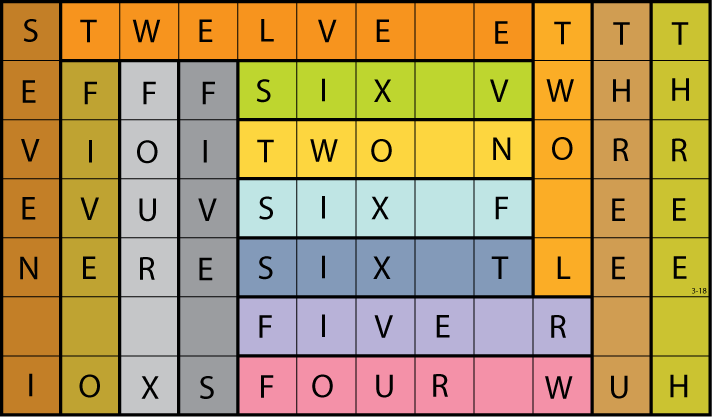
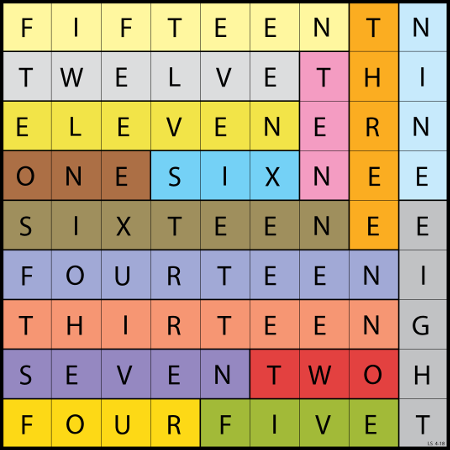
Lee Sallows sent this self-descriptive rectangle tiling: The grid catalogs its own contents by arranging its 70 letters and 14 spaces into 14 itemizing phrases.
Bonus: The rectangle measures 7 × 12, which is commemorated by the two strips that meet in the top left-hand corner. And “The author’s signature is also incorporated.”
(Thanks, Lee!)
A Clueless Crossword
Podcast Episode 158: The Mistress of Murder Farm

Belle Gunness was one of America’s most prolific female serial killers, luring lonely men to her Indiana farm with promises of marriage, only to rob and kill them. In this week’s episode of the Futility Closet podcast we’ll tell the story of The LaPorte Black Widow and learn about some of her unfortunate victims.
We’ll also break back into Buckingham Palace and puzzle over a bet with the devil.
Double Alphamagic Squares
In 1986 British electronics engineer Lee Sallows invented the alphamagic square:
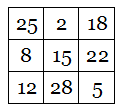
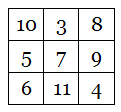
As in an ordinary magic square, each row, column, and long diagonal produces the same sum. But when the number in each cell is replaced by the length of its English name (25 -> TWENTY-FIVE -> 10), a second magic square is produced:
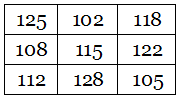
Now British computer scientist Chris Patuzzo, who found the percentage-reckoned pangram that we covered here in November 2015, has created a double alphamagic square:

Each row, column, and long diagonal here totals 303370120164. If the number in each cell is replaced by the letter count of its English name (using “and” after “hundred,” e.g. ONE HUNDRED AND FORTY-EIGHT BILLION SEVEN HUNDRED AND TWENTY-EIGHT MILLION THREE HUNDRED AND SEVENTY-EIGHT THOUSAND THREE HUNDRED AND SEVENTY-EIGHT), then we get a new magic square, with a common sum of 345:
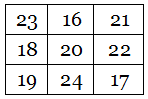
And this is itself an alphamagic square! Replace each number with the length of its name and you get a third magic square, this one with a sum of 60:
Chris has found 50 distinct doubly alphamagic squares, listed here. I suppose there must be some limit to this — is a triple alphamagic square even possible?
(Thanks, Chris and Lee.)
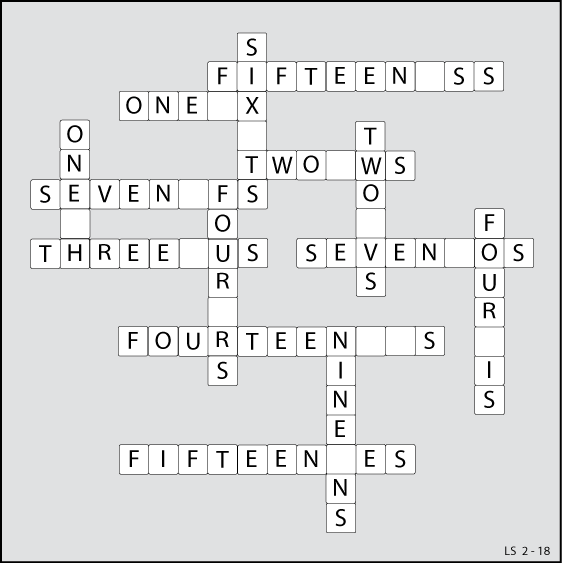
Self-Descriptive Squares
Lee Sallows has been working on a new experiment in self-reference that he calls self-descriptive squares, arrays of numbers that inventory their own contents. Here’s an example of a 4×4 square:

The sums of the rows and columns are listed to the right and below the square. These sums also tally the number of times that each row’s rightmost entry, or each column’s lowermost entry, appears in the square. So, for example, the sum of the top row is 3, and that row’s rightmost entry is 1; correspondingly, the number 1 appears three times in the square. Likewise, the sum of the rightmost column is 2, and the lowermost entry in that column, 4, appears twice in the square.
In this example this property extends to the diagonals — and, pleasingly, each sum applies to both ends of its diagonal. The northwest-southeast diagonal totals 2, and both -2 and 4 appear twice in the square. And the southwest-northeast diagonal totals 3, and both 1 and 0 appear three times.
“Easy to understand, but not so easy to produce!” he writes. “I’m still in the throes of figuring out the surprisingly complicated theory of such squares. It turns out there are just two basic squares of 3×3. One of them can be found at the centre of this 5×5 example, which is therefore a concentric self-descriptive square:”

(Thanks, Lee.)
A Reflexive Rainbow
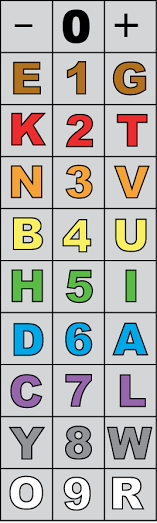
From Lee Sallows: The international color code is used to mark the values of electronic components such as resistors. It assigns a distinct color to each of the 10 decimal digits, as seen in the center column of the table at right: 0 = BLACK, 1 = BROWN, …, 9 = WHITE.
Lee’s table has an ingenious reflexive property. The letters in the left-hand column are associated with the values -1 to -9, and those in the right-hand column with the values 1 to 9.
Now spelling the name of each color produces a sum that matches the number represented by that color:

“This is more remarkable that it may seem,” Lee writes, “because the numbers assigned to the letters are now restricted to single-digit values only.”
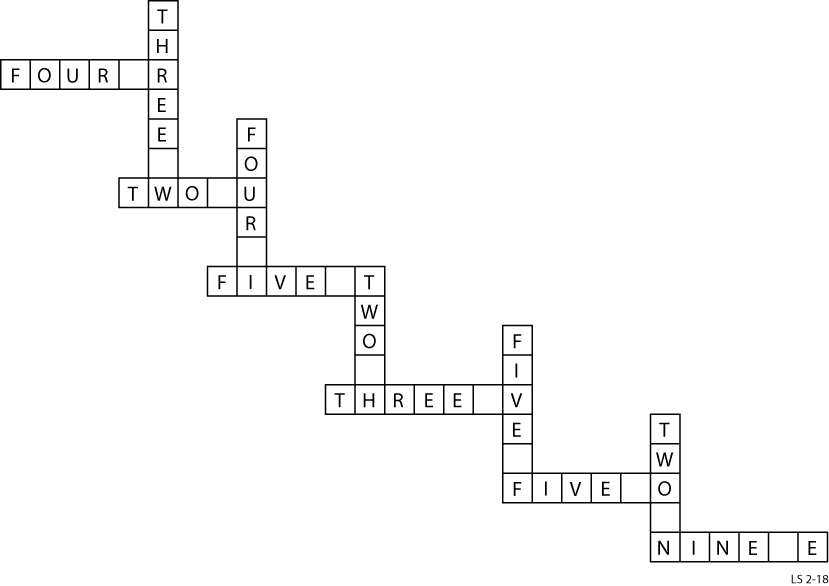
A Self-Enumerating Crossword

Here’s a unique crossword puzzle by Lee Sallows. There are no clues — instead, each of the 12 entries must take the form [NUMBER](space)[LETTER](S), like so:
EIGHT BS
NINETEEN XS
ONE J
And so on. Can you complete the puzzle so that the finished grid presents an inventory of its own contents?
(A couple observations to get you started: Because the puzzle contains 12 entries, the solution will use only 12 letters. And one useful place to start is the shortest “down” entry, which is too short to be plural — it must be “ONE [LETTER]”.)
A New Pangram
British recreational mathematician Lee Sallows has produced many varieties of the self-enumerating pangram — sentences that inventory their own contents:
This pangram contains four As, one B, two Cs, one D, thirty Es, six Fs, five Gs, seven Hs, eleven Is, one J, one K, two Ls, two Ms, eighteen Ns, fifteen Os, two Ps, one Q, five Rs, twenty-seven Ss, eighteen Ts, two Us, seven Vs, eight Ws, two Xs, three Ys, & one Z.
A few years ago he began to wonder whether it’s possible to produce a sentence that reckons its totals as percentages. This is more difficult, because the percentages won’t always work out to be integers. As he worked on the problem he mentioned it to a few others, among them British computer scientist Chris Patuzzo. And a few days ago, Patuzzo sent him this:
This sentence is dedicated to Lee Sallows and to within one decimal place four point five percent of the letters in this sentence are a’s, zero point one percent are b’s, four point three percent are c’s, zero point nine percent are d’s, twenty point one percent are e’s, one point five percent are f’s, zero point four percent are g’s, one point five percent are h’s, six point eight percent are i’s, zero point one percent are j’s, zero point one percent are k’s, one point one percent are l’s, zero point three percent are m’s, twelve point one percent are n’s, eight point one percent are o’s, seven point three percent are p’s, zero point one percent are q’s, nine point nine percent are r’s, five point six percent are s’s, nine point nine percent are t’s, zero point seven percent are u’s, one point four percent are v’s, zero point seven percent are w’s, zero point five percent are x’s, zero point three percent are y’s and one point six percent are z’s.
Details are here. The next challenge is a version where the percentages are accurate to two decimal places — Patuzzo is working on that now.
(Thanks, Lee.)