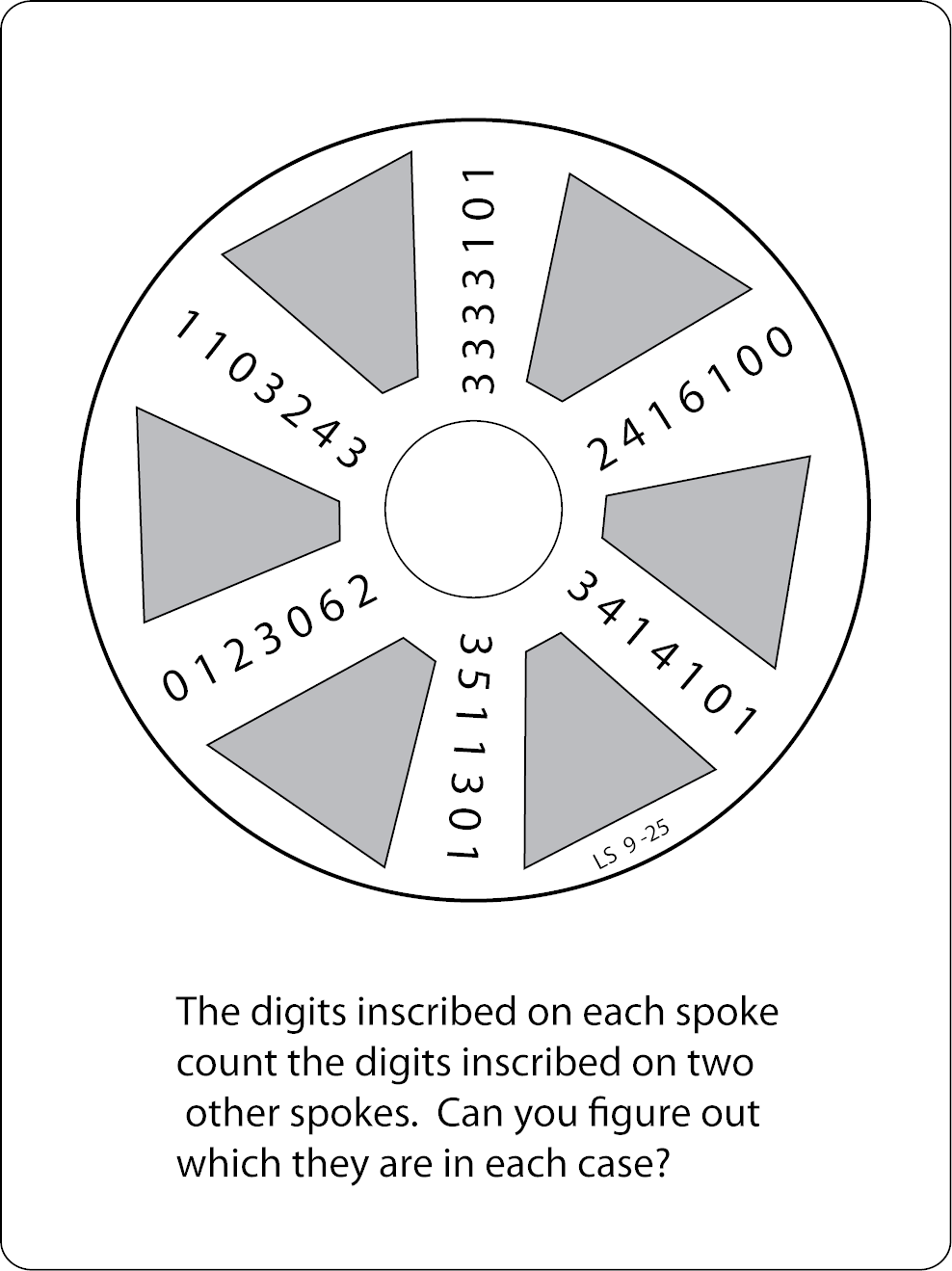
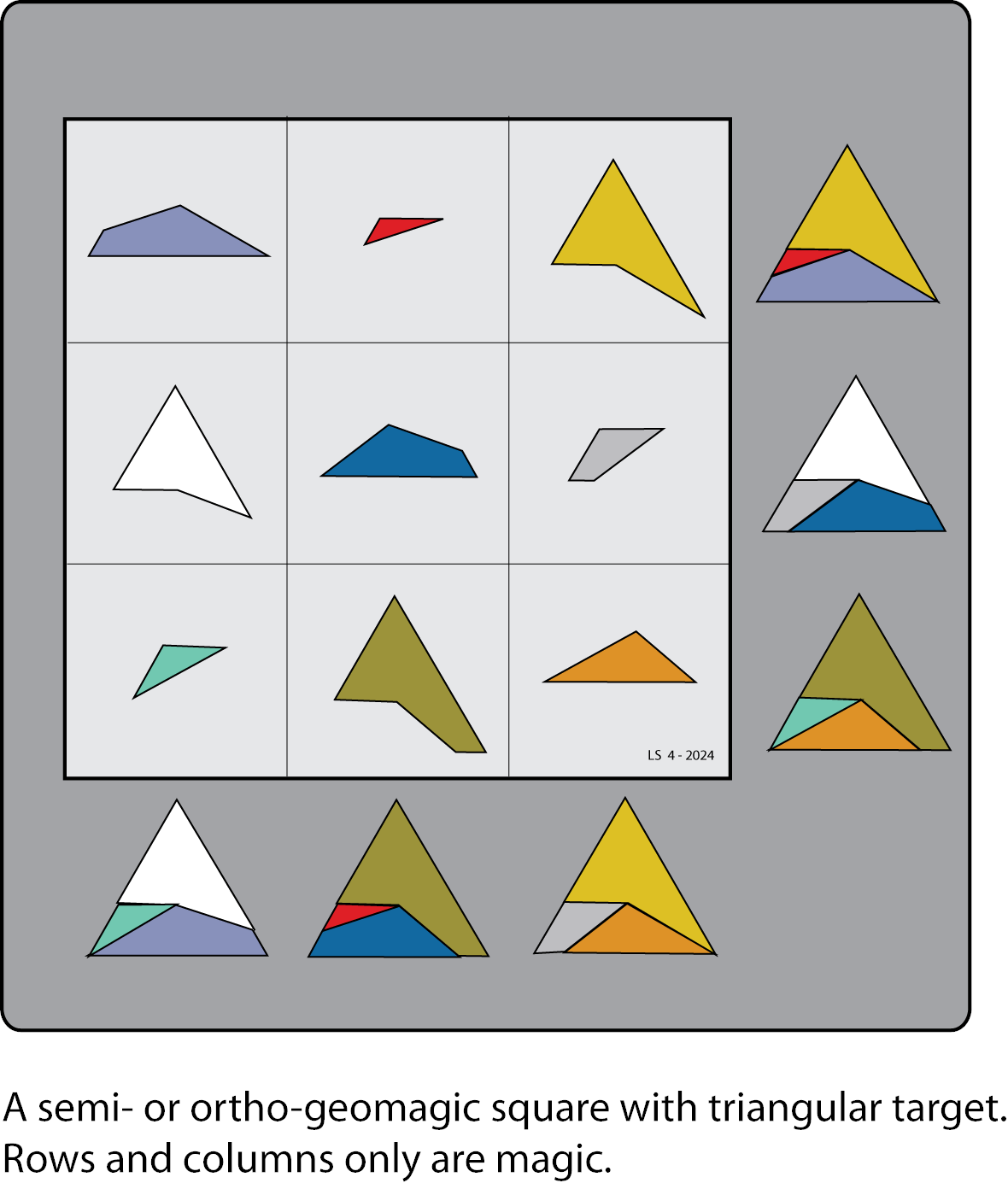
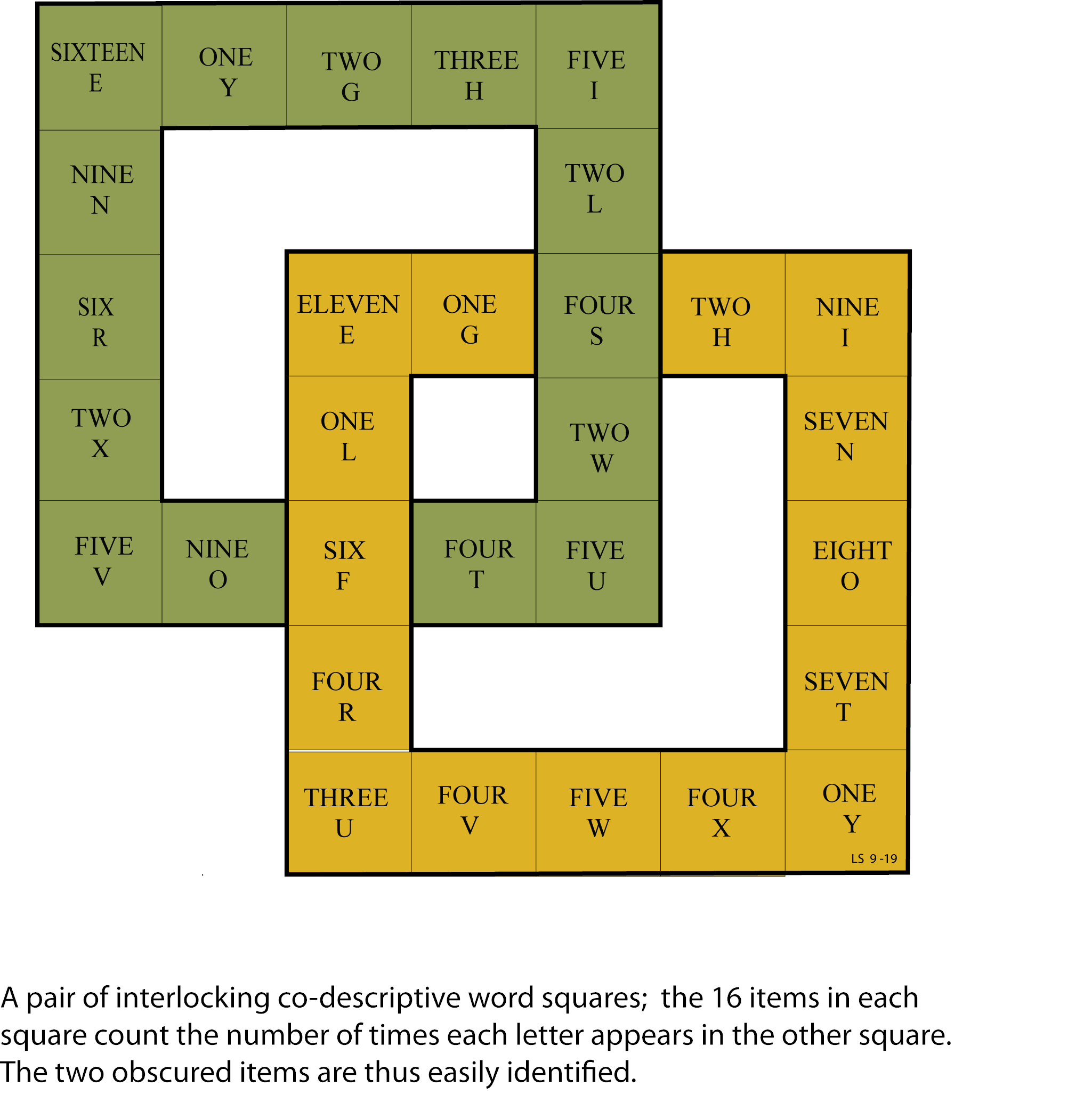
Search Results for: lee sallows
Geomagic
A Self-Intersecting Reflexicon
A Perpetual Motion Device
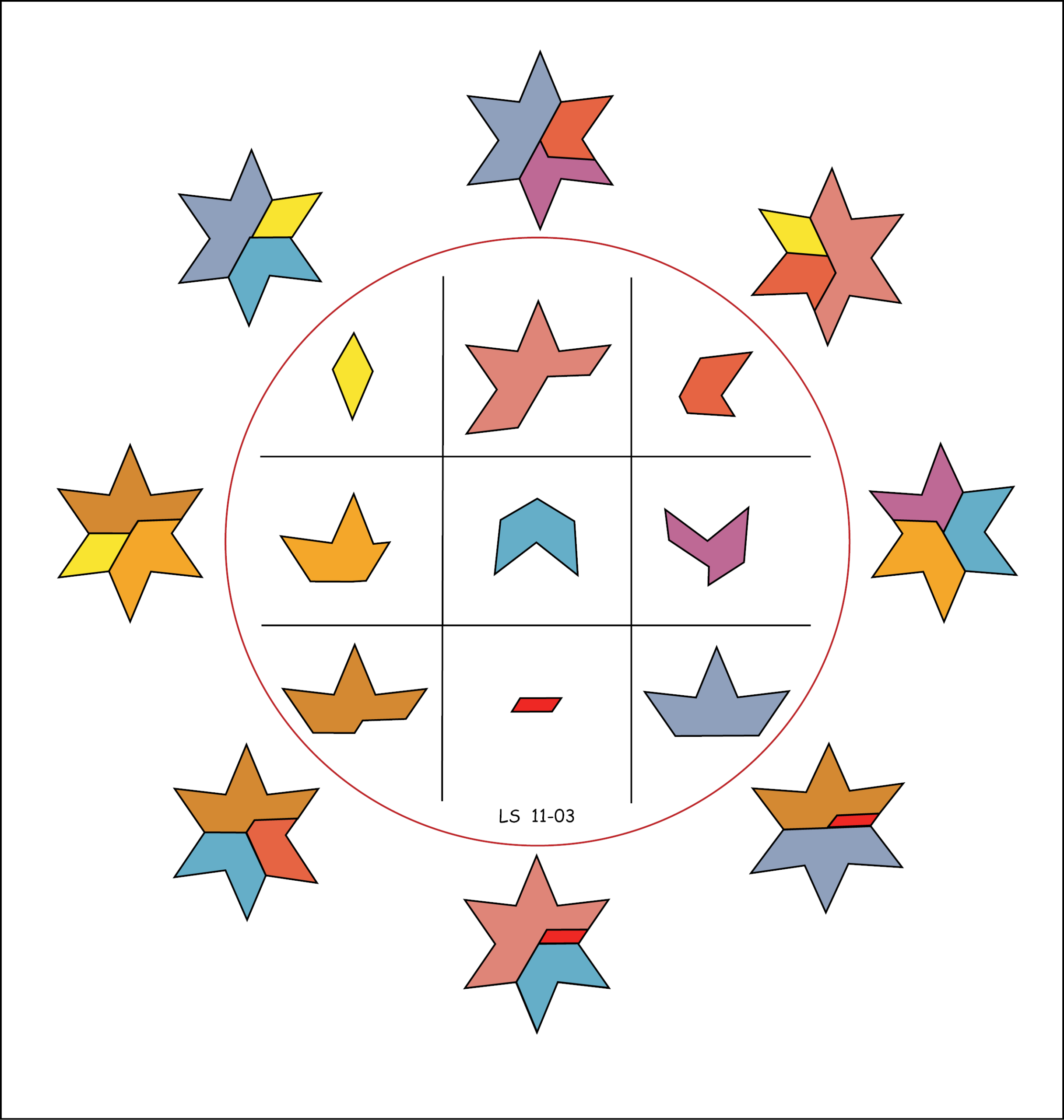
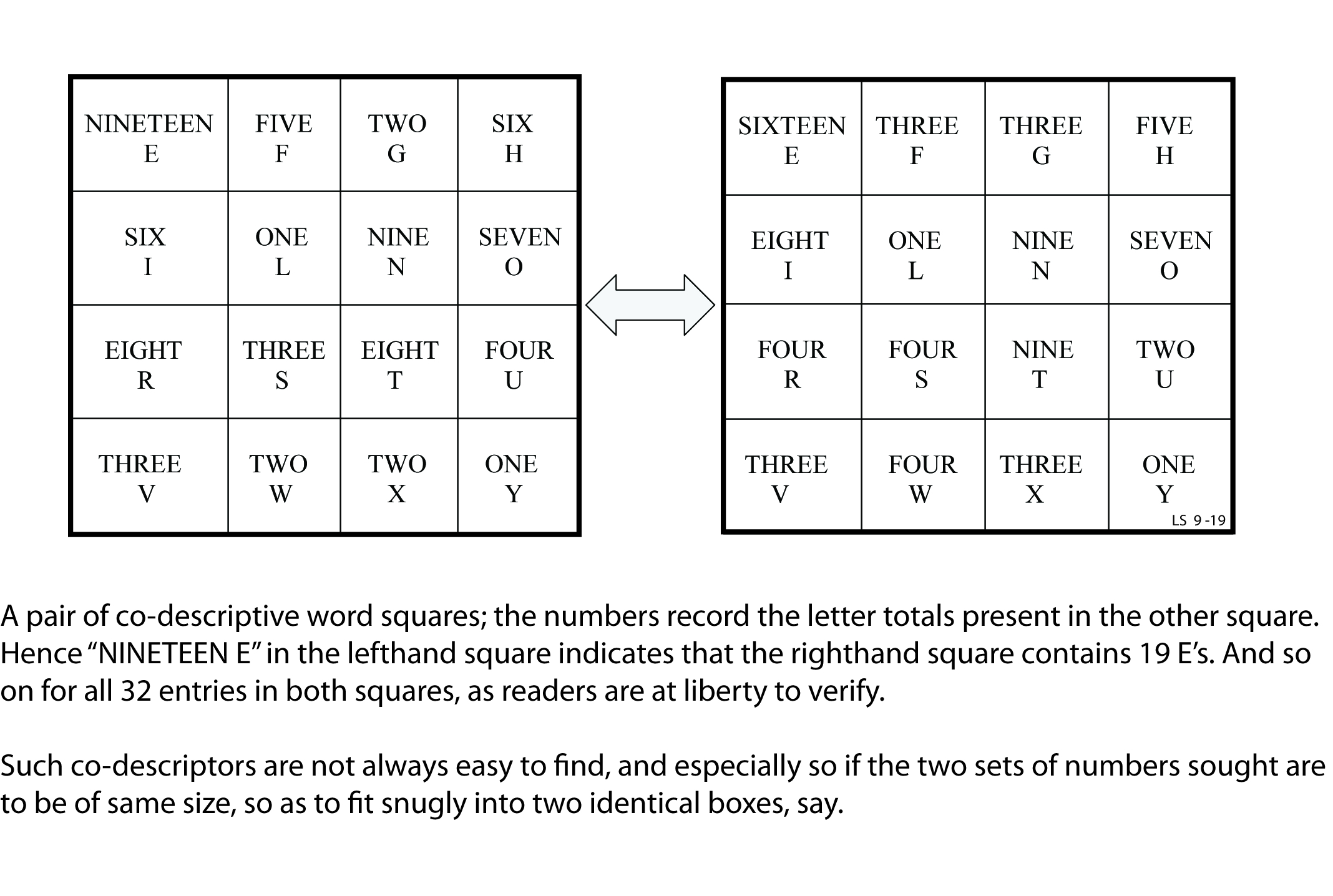
A 3×3 Panmagic Square
From Lee Sallows:
Numerical panmagic squares of 3×3 being impossible, the above square is in fact the first known order-3 panmagic square, a boast it can enjoy until the day that someone comes up with an improved solution. Such as one using all nine connected pieces, say.
Or not, perhaps? For the square above has a further property that other panmagic squares may not possess. Choose any three of the four corner pieces. There are four possibilities: aci, cig, agi and acg. Whatever your choice, the three pieces selected will tile the target.
(Thanks, Lee!)