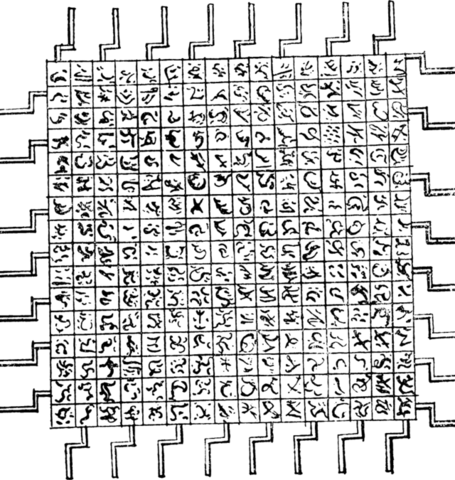
Song of a neighborhood nightingale transcribed in 1868 by German naturalist Johann Matthäus Bechstein:
Tioû, tioû, tioû, tioû.
Spe, tiou, squa.
Tiô, tiô, tiô, tiô, tio, tio, tio, tix.
Coutio, coutio, coutio, coutio.
Squô, squô, squô, squô.
Tzu, tzu, tzu, tzu, tzu, tzu, tzu, tzu, tzu, tzi.
Corror, tiou, squa pipiqui.
Zozozozozozozozozozozozo, zirrhading!
Tsissisi, tsissisisisisisisis.
Dzorre, dzorre, dzorre, dzorre, hi.
Tzatu, tzatu, tzatu, tzatu, tzatu, tzatu, tzatu, dzi.
Dlo, dlo, dlo, dlo, dlo, dlo, dlo, dlo, dlo.
Quio, tr rrrrrrrr itz.
Lu, lu, lu, lu, ly, ly, ly, liê, liê, liê, liê.
Quio, didl, li lulylie.
Hagurr, gurr quipio!
Coui, coui, coui, coui, qui, qui, qui, qui, gai, gui, gui, gui.
Goll goll goll goll guia hadadoi.
Couigui, horr, he diadia dill si!
Hezezezezezezezezezezezezezezezeze couar ho dze hoi.
Quia, quia, quia, quia, quia, quia, quia, quia, ti.
Ki, ki, ki, ïo, ïo, ïo, ioioioio ki.
Lu ly li le lai la leu lo, didl ïo quia.
Kigaigaigaigaigaigaigai guiagaigaigai couior dzio dzio pi.
In his 1795 Natural History of Cage Birds, he notes that some captive birds “never sing unless confined within narrow limits, being obliged, as it would appear, to solace themselves, for the want of liberty, with their song,” and so should never be given freedom within a room.
See Bird Talk, Bird Songs, and Who’s Who.