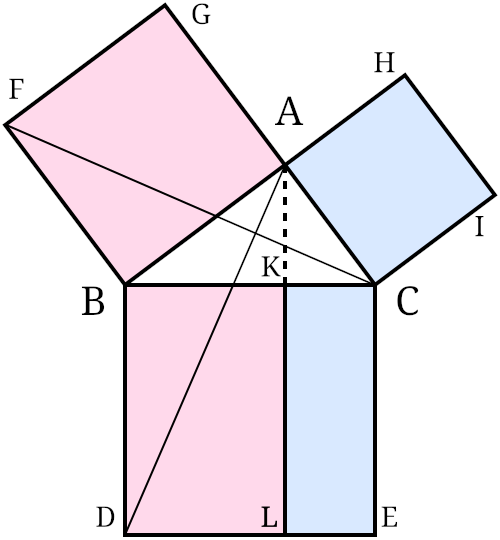
This is Euclid’s proof of the Pythagorean theorem — Schopenhauer called it a “brilliant piece of perversity” for its needless complexity:

1. Erect a square on each leg of a right triangle. From the triangle’s right angle, A, draw a line parallel to BD and CE. This will intersect BC and DE perpendicularly at K and L.
2. Draw segments CF and AD, forming triangles BCF and BDA.
3. Because angles CAB and BAG are both right angles, C, A, and G are collinear.
4. Because angles CBD and FBA are both right angles, angle ABD equals angle FBC, since each is the sum of a right angle and angle ABC.
5. Since AB is equal to FB, BD is equal to BC, and angle ABD equals angle FBC, triangle ABD is congruent to triangle FBC.
6. Since A-K-L is a straight line that’s parallel to BD, rectangle BDLK has twice the area of triangle ABD, because they share base BD and have the same altitude, BK, a line perpendicular to their common base and connecting parallel lines BD and AL.
7. By similar reasoning, since C is collinear with A and G, and this line is parallel to FB, square BAGF must be twice the area of triangle FBC.
8. Therefore, rectangle BDLK has the same area as square BAGF, AB².
9. By applying the same reasoning to the other side of the figure, it can be shown that rectangle CKLE has the same area as square ACIH, AC².
10. Adding these two results, we get AB² + AC² = BD × BK + KL × KC.
11. Since BD = KL, BD × BK + KL × KC = BD(BK + KC) = BD × BC.
12. Therefore, since CBDE is a square, AB² + AC² = BC².

The diagram became known as the bride’s chair due to a confusion in translation between Greek and Arabic.