It appears that there was a club and the president decided that it would be nice to hold a dinner for all the members. In order not to give any one member prominence, the president felt that they should be seated at a round table. But at this stage he ran into some problems. It seems that the club was not all that amicable a little group. In fact each member only had a few friends within the club and positively detested all the rest. So the president thought it necessary to make sure that each member had a friend sitting on either side of him at the dinner. Unfortunately, try as he might, he could not come up with such an arrangement. In desperation he turned to a mathematician. Not long afterwards, the mathematician came back with the following reply. ‘It’s absolutely impossible! However, if one member of the club can be persuaded not to turn up, then everyone can be seated next to a friend.’ ‘Which member must I ask to stay away?’ the president queried. ‘It doesn’t matter,’ replied the mathematician. ‘Anyone will do.’

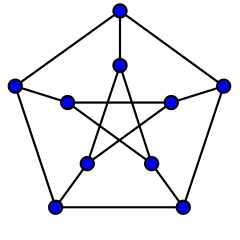
This problem, dubbed “Le Cercle Des Irascibles,” was posed by René Sousselier in Revue Française de Recherche Opérationelle in 1963. The remarkable solution was given the following year by J.C. Herz. In this figure, it’s possible to visit all 10 nodes while traveling on line segments alone, but there’s no way to close the loop and return to the starting node at the end of the trip (and thus to seat all the guests at a round table). But if we remove any node (and its associated segments), the task becomes possible. In the language of graph theory, the “Petersen graph” is the smallest hypohamiltonian graph — it has no Hamiltonian cycle, but deleting any vertex makes it Hamiltonian.

(Translation by D.A. Holton and J. Sheehan.)