One other interesting item from Paul Halmos’ Problems for Mathematicians, Young and Old (1991): Pick a point in the first quadrant and draw a downward-sloping line through it. This line makes a triangle with the coordinate axes. At what angle should we set the line to minimize the area of the triangle?

This problem yields to calculus, but there’s a simple geometric solution. Reflect the axes through the point to make a box:

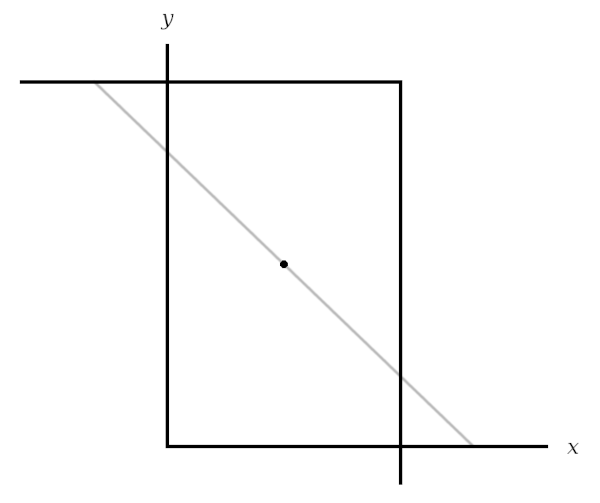
Now as we swivel our line through the point, it defines two triangles, one against each set of axes. The area of the combined triangles is equal to or greater than the area of the box. So, intuitively, it reaches a minimum just as the swiveling line becomes a diagonal of the box. That’s the answer.