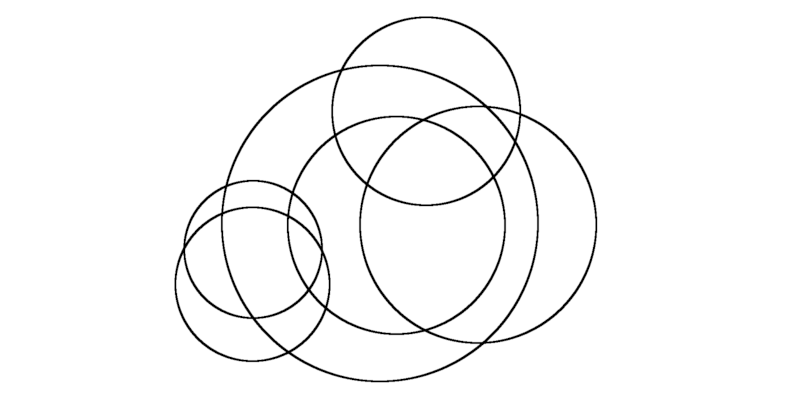
A bit more on map coloring: Suppose a map consists of a number of overlapping circles, like this, so that the borders of each “country” are all arcs of circles. How many colors would we need to color this map, again with the proviso that no two countries that share a border will receive the same color?

Here we need only two. Each country occupies the interior of some number of circles. If that number is even, color the country white; if odd, black. Crossing a border always changes the number by 1, so each border will divide countries of opposite colors.

From Paul R. Halmos, Problems for Mathematicians, Young and Old, 1991.