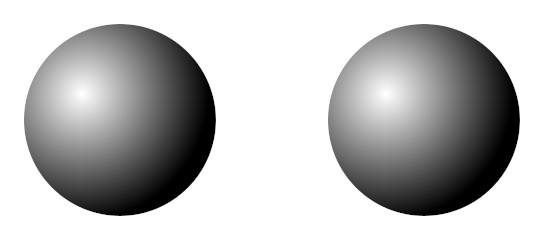
Gottfried Leibniz held that no two distinct objects can have exactly the same properties.

But, Max Black asked, “Isn’t it logically possible that the universe should have contained nothing but two exactly similar spheres? We might suppose that each was made of chemically pure iron, had a diameter of one mile, that they had the same temperature, colour, and so on, and that nothing else existed. Then every quality and relational characteristic of the one would also be a property of the other.”

(We might object that the two spheres are discernible because they occupy different positions in space, but this is true only if we have a third object to use as a reference point in establishing the “objective” location of each sphere. If the only things in the universe are the two spheres, then their positions can be established only in relation to each other, and these would always be identical — for example, each sphere is five miles from another sphere.)

“Now if what I am describing is logically possible,” wrote Black, “it is not impossible for two things to have all their properties in common.”

Sort of vaguely related:

On a visit to Princeton, E.H. Moore began a lecture by saying, “Let a be a point and let b be a point.”

Solomon Lefschetz asked, “But why don’t you just say, ‘Let a and b be points’?”

Moore said, “Because a may equal b.”

In Indiscrete Thoughts, Gian-Carlo Rota writes, “Lefschetz got up and left the lecture room.” Rota calls this “an example of mathematical pedantry.”

(Max Black, “The Identity of Indiscernibles,” Mind 61:242 [April 1952], 153-164.)