A brainteaser by S. Ageyev, from the November-December 1991 issue of Quantum:
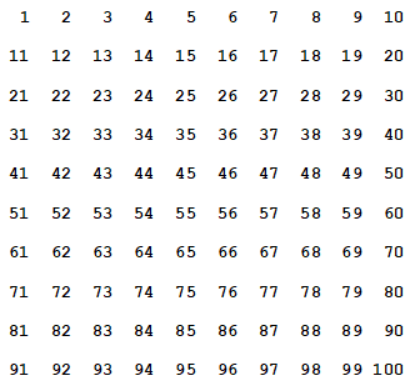
Suppose that we change the signs of 50 of these numbers such that exactly half the numbers in each row and each column get a minus sign. Prove that the sum of all the numbers in the resulting table is zero.
|
SelectClick for Answer |
Call the original table A and represent it as the sum of two tables B and C:
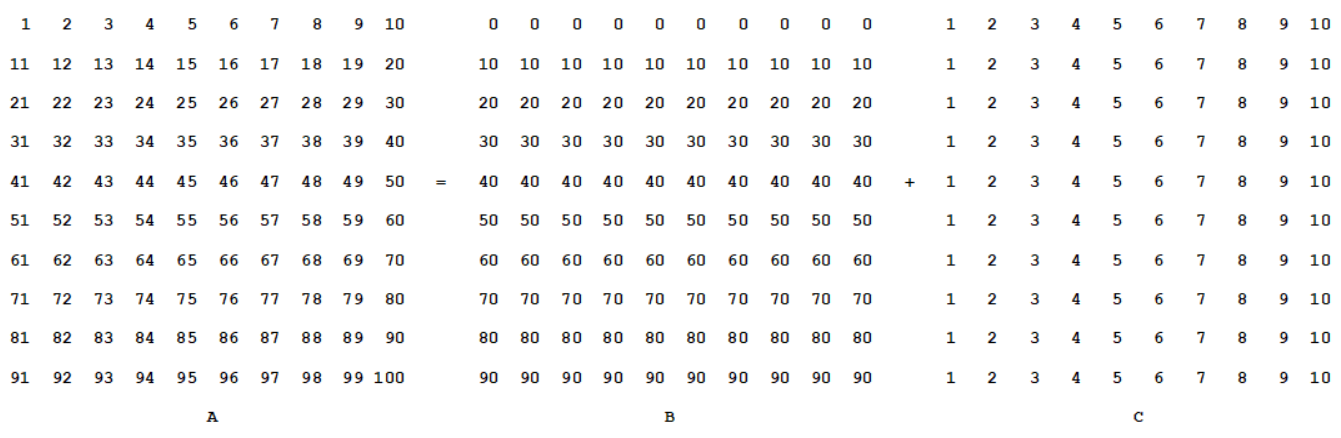
Now if we assign minus signs correspondingly to all three tables as described in the problem, then the sum of each row in Table B and each column in Table C will be zero. It follows that the sum of all the numbers in Tables B and C combined, and hence in Table A, is zero.
|


