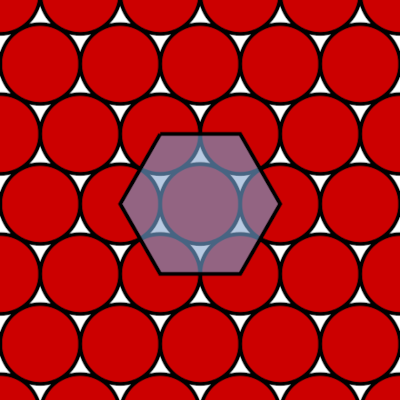
Can any 10 points on a plane always be covered with some number of nonoverlapping unit discs?

It’s not immediately clear that the answer is yes. The most efficient way to pack circles together on the plane is the hexagonal packing shown above; it covers about 90.69 percent of the surface. But if our 10 points are inconveniently arranged, it’s not clear that we’ll always be able to shift the array of circles around in order to get them all covered.

In this case there’s a neat proof that takes advantage of a technique called the probabilistic method — if, for a group of objects, the probability is less than 1 that a randomly chosen object does not have a certain property, then there must exist an object that has this property.

Take a hexagonal packing randomly. Then, for any point on the plane, the probability that it’s not covered by the chosen packing is about 1 – 0.9069 = 0.0931. This means that for any 10 points, the chance that one or more points are not covered is approximately 0.0931 × 10 = 0.931. And that’s less than 1.

“Therefore, we obtain from the principle that there exists some closest packing that covers all the 10 points,” writes mathematician Hirokazu Iwasawa of the Institute of Actuaries of Japan. “And, in such a packing, we actually need at most 10 discs to cover the 10 points.”

(Hirokazu Iwasawa, “Using Probability to Prove Existence,” Mathematical Intelligencer 34:3 [September 2012], 11-14. The puzzle was created by Naoki Inaba.)