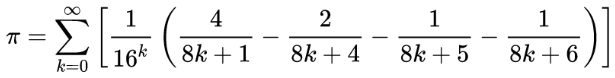
Here’s something remarkable: This formula, discovered in 1995 by David Bailey, Peter Borwein, and Simon Plouffe of the University of Quebec at Montreal, permits the calculation of isolated digits of π — it’s possible to calculate, say, the trillionth digit of π without working out all the preceding digits.

The catch is that it works only in base 2 (binary) and base 16 (hexadecimal), but not in base 10. So it’s possible to know, say, that the five trillionth binary digit of π is 0, but there’s no way to convert the result into its decimal equivalent without working out all the intervening binary digits.

“The new formula allows the calculation of the nth base 2 or base 16 digit of π in a time that is essentially linear in n, with memory requirements that grow logarithmically (very slowly) in n,” writes David Darling in The Universal Book of Mathematics. “One possible use of the Bailey-Borwein-Plouffe formula is to help shed light on whether the distribution of π’s digits are truly random, as most mathematicians suppose.”

08/14/2022 UPDATE: A new formula permits the extraction of decimal digits. (Thanks, Edward.)