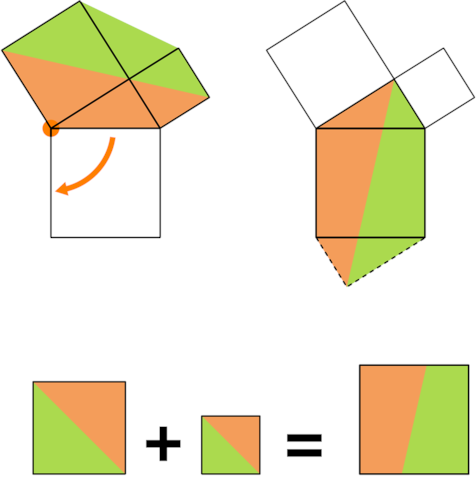
This pretty proof of the Pythagorean theorem is attributed to Leonardo da Vinci. Draw a right triangle and construct a square on each side, and make a copy of the original triangle and add it to the bottom of the hypotenuse square as shown. Now the shaded hexagon in the first figure can be rotated 90 degrees clockwise around the indicated point to occupy the position shown in the second figure. The orange and green quadrilaterals in the second figure are seen to be congruent to those in the first figure: The three shortest sides of the orange quadrilateral in the second figure correspond to their counterparts in the first, and the angles between them are assembled from the same constituents. The same is true of the green quadrilaterals. In each figure the shaded hexagon contains two instances of the original right triangle; remove these and we can see that the two squares in the first figure equal the large square in the second figure, proving Pythagoras.

10/10/2021 UPDATE: A number of readers point out that only the orange quadrilateral here can properly be said to turn; in the second diagram the green quadrilateral has been reflected as well. (Thanks, Mark and Bill.)