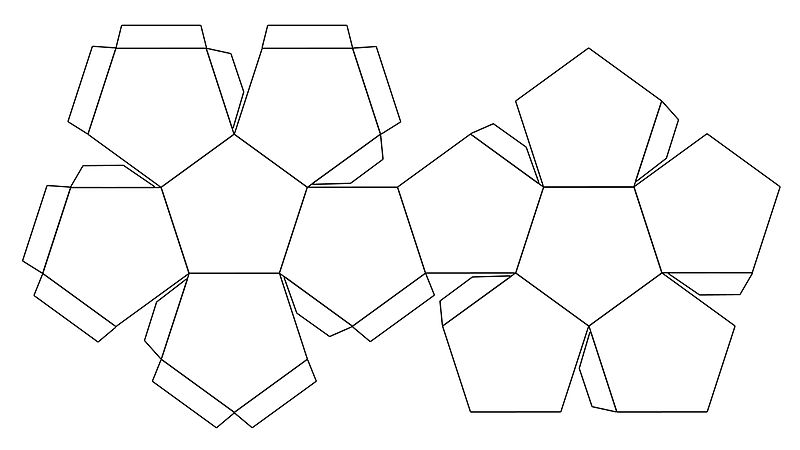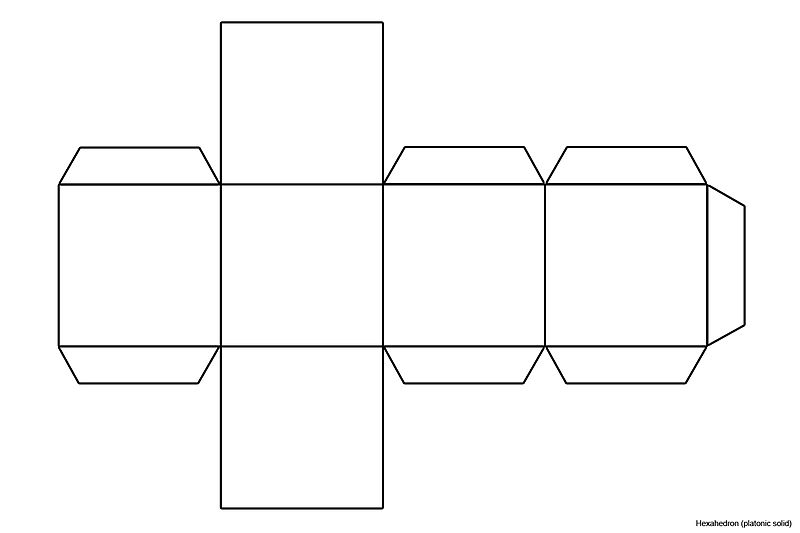
A neat little fact pointed out by George Pólya and Donald Coxeter: If a convex polyhedron is unfolded and presented as a flat “net” fitted with tabs for gluing, as in a children’s activity book, the smallest number of tabs needed is just one less than the number of vertices in the assembled shape. The net above, with 7 tabs, can be assembled into a hexahedron with 8 vertices, and the one below, with 19 tabs, can be assembled into a dodecahedron with 20.

(Nick Lord, “Nets and Tabs,” Mathematical Gazette 73:464 [June 1989], 93-96.)