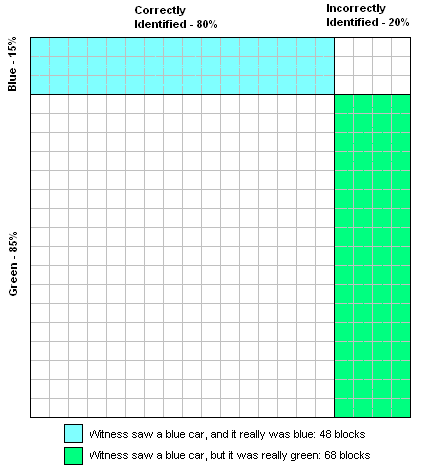
A cab was involved in a hit and run accident at night. Two cab companies, the Green and the Blue, operate in the city. 85% of the cabs in the city are Green and 15% are Blue.

A witness identified the cab as Blue. The court tested the reliability of the witness under the same circumstances that existed on the night of the accident and concluded that the witness correctly identified each one of the two colors 80% of the time and failed 20% of the time.

What is the probability that the cab involved in the accident was Blue rather than Green knowing that this witness identified it as Blue?

Psychologists Amos Tversky and Daniel Kahneman offered this problem to study subjects in 1972. The right answer is about 41 percent:

• There’s a 12% chance (15% times 80%) of the witness correctly identifying a blue cab.
• There’s a 17% chance (85% times 20%) of the witness incorrectly identifying a green cab as blue.
• Thus there’s a 29% chance (12% plus 17%) that the witness will identify the cab as blue.
• And that means there’s approximately a 41% chance (12% divided by 29%) that the cab identified as blue is really blue:

Most subjects estimated the probability at more than 50 percent, some more than 80 percent.

Tversky and Kahneman call this the representativeness heuristic: When we rely on representativeness to make a judgment, we tend to judge wrongly because the fact that a thing is more representative doesn’t make it more likely.

(Amos Tversky and Daniel Kahneman, “Evidential Impact of Base Rates,” No. TR-4, Stanford University Department of Psychology, 1981.)