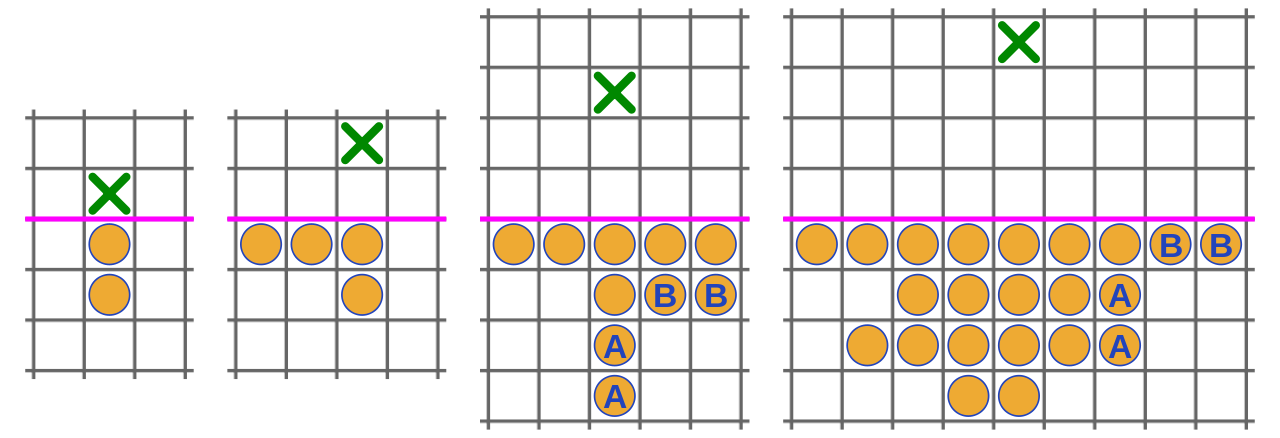
Mathematician John Horton Conway invented this game in 1961. A line divides an infinite checkerboard into two territories. An army of soldiers occupies the lower territory, one per cell. They want to deliver a man as far as possible into the upper territory, but they can proceed only as in peg solitaire: One soldier jumps orthogonally over another soldier and lands on an empty square immediately beyond him, whereupon the “jumped” man is removed.

It’s immediately obvious how the soldiers can get a man into the upper territory, and it’s fairly clear how they can get one as far as the fourth row above the line. But, surprisingly, Conway proved that that’s the limit: No matter how they arrange their efforts, the soldiers cannot get a man beyond that row in a finite number of moves.

Christopher, the 15-year-old hero of Mark Haddon’s 2003 novel The Curious Incident of the Dog in the Night-Time, says that Conway’s Soldiers is “a good maths problem to do in your head when you don’t want to think about something else because you can make it as complicated as you need to fill your brain by making the board as big as you want and the moves as complicated as you want.”

You can find any number of proofs online, but the most convincing way to see that the task is impossible is to try it yourself.