Odd at Heart - Futility Closet

A problem proposed by Charles W. Trigg in the Spring 1970 issue of the Pi Mu Epsilon Journal (Volume 5, Number 4):

The digits 1-9 can be arranged in a square array so that the digits in no column, row, or long diagonal appear in order of magnitude:

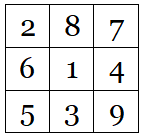
trigg pmej paritypuzzle

Prove that, however this is done, the central digit must be odd.

	Select Click for Answer
One row, one column, and two diagonals pass through the center. In order to honor the requirement, we must arrange the eight outer digits so that none of these four triplets falls in ascending or descending order; that is, in each of these four triplets the center digit must be either the highest or the lowest value. In order to accomplish this, we must complete each triplet by adding two digits that are either both lower than the central digit or both higher. But if the center digit is even, that leaves us with an odd number of digits whose value is lower than the center digit and an odd number whose value is higher. So we’ll be forced to complete at least one of the four triplets by combining one higher and one lower value — producing a trio that falls in order of magnitude.