In “The Adventure of the Final Problem,” Sherlock Holmes flees London, pursued by his archenemy, James Moriarty. Both are headed to Dover, where Holmes hopes to escape to the continent, but there’s one intermediate stop available, at Canterbury. Holmes faces a choice: Should he get off at Canterbury or go on to Dover? If Moriarty finds him at either station he’ll kill him.

In their 1944 Theory of Games and Economic Behavior, mathematician John von Neumann and economist Oskar Morgenstern address this as a problem in game theory. They set up the following payoff matrix showing Moriarty’s calculations:

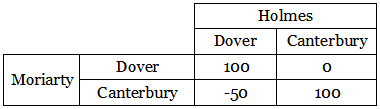
Von Neumann and Morgenstern conclude that “Moriarty should go to Dover with a probability of 60%, while Sherlock Holmes should stop at the intermediate station with a probability of 60% — the remaining 40% being left in each case for the other alternative.”

As it turns out, that’s exactly what happens in the story — Holmes and Watson get out at Canterbury and watch Moriarty’s train roar past toward Dover, “beating a blast of hot air into our faces.” “There are limits, you see, to our friend’s intelligence,” Holmes tells Watson. “It would have been a coup-de-maître had he deduced what I would deduce and acted accordingly.”

(It’s not quite that simple — in a footnote, von Neumann and Morgenstern point out that Holmes has excusably replaced the 60% probability with certainty in his calculations. In fact, they say, the odds favor Moriarty — “Sherlock Holmes is as good as 48% dead when his train pulls out from Victoria Station.”)