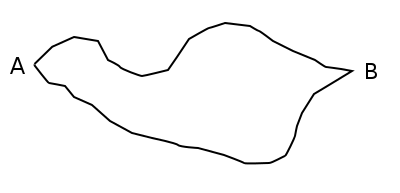
Towns A and B are connected by two roads. Suppose that two cars connected by a rope of length 2r can travel from A to B without breaking the rope. How can we prove that two circular wagons of radius r, moving along these roads in opposite directions, will necessarily collide?

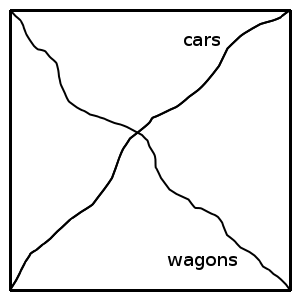
This can be solved neatly by creating a configuration space. Map each road onto a unit segment, and set these up as two sides of a square. The northern car’s progress is reflected by a point moving up the left side of the square, and the southern car’s by a point moving from left to right along the bottom. Now the motion of the two cars from A to B is represented by a continuous curve connecting (0,0) and (1,1).

The wagons start from opposite towns, so their motion is represented by a curve from (0,1) to (1,0), and it’s immediately clear that the two curves must intersect. The intersection point corresponds to the collision of the wagons.

This example, by N. Konstantinov, is reportedly common in Russian mathematical folklore; I found it in Serge Tabachnikov’s 2005 book Geometry and Billiards (of all places).