The men sold x cows for $x, so their income from that sale is $x². x² isn’t divisible by 12, so x can’t be a multiple of 6 (if it were, then x² would be divisible by 36 and hence by 12). So x is 12n ± y, where n is any integer and y is an integer from 1 to 5.

Each man ends up with the same number of animals, so the total number of animals must be even, which means there’s an odd number of sheep and one lamb. So (12n ± y)² when divided by 12 should leave a remainder and have an odd integer for its quotient.

12n² ± 2ny will always be even, so that last term, y²/12, must provide an odd contribution toward this quotient. In order to do this, y² must exceed 12, so y must be 4 or 5. If it’s 5, we get

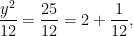
which provides an even contribution (2) to the quotient. So y must be 4 and y² = 16:

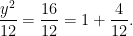
That’s what we need; the integer part of this quotient, 1, is odd. Since the remainder when 4² is divided by 12 is 4, a lamb costs $4. Consequently, in dividing the flock one man got a $4 lamb and the other got a $12 sheep. To make this fair, the traded harmonica must be worth $4.

(The problem was proposed by J.H. Neelley, T.L. Smith, and P.S. Ganesa Sastri in AMM 37:3, 162; Ross Honsberger introduced the harmonica in recounting it in his Mathematical Morsels, 1978. This solution is by P.S. Ganesa Sastri of Trichinopoly, South India.)