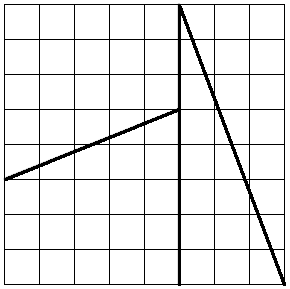
This square of 8 × 8 = 64 square units can apparently be reassembled into a rectangle of 5 × 13 = 65 square units:

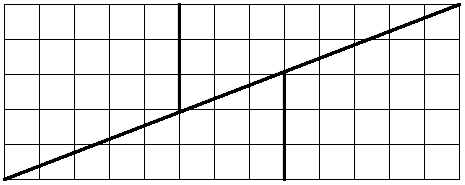
This paradox is described in W.W. Rouse Ball’s 1892 Mathematical Recreations and Essays; it seems to have been published first in 1868 in Zeitschrift für Mathematik und Physik.

In 1938 the Rockefeller Foundation’s Warren Weaver discovered an old trove of papers from the 1890s in which Lewis Carroll puzzled out the dimensions of all possible squares in which this illusion is possible (the other sizes include squares of 21 and 55 units on a side).

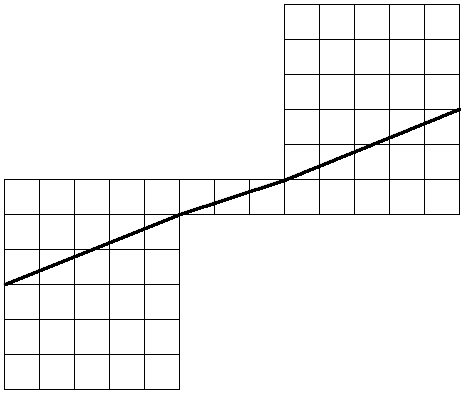
Regardless of publication, it’s not clear who first came up with the idea. Sam Loyd claimed to have presented it to the American Chess Congress in 1858. That would be interesting, as it was his son who later discovered that the four pieces can be assembled into a figure of 63 squares:

(Warren Weaver, “Lewis Carroll and a Geometrical Paradox,” American Mathematical Monthly 45:4 [April 1938], 234-236.)