A spelling net is the pattern made when one writes down one instance of each unique letter that appears in a word and then connects these letters with lines, spelling out the word. For instance, the spelling net for VIVID is made by writing down the letters V, I, and D and drawing a line from V to I, I to V, V to I, and I to D.

Different words produce different spelling nets, of course, but every spelling net is an example of a graph, a collection of points connected by lines. A graph is said to be non-planar if some of the lines must cross; in the case of the spelling net, this means that no matter how we arrange the letters on the page, when we connect them in order we find that at least two of the lines must cross.

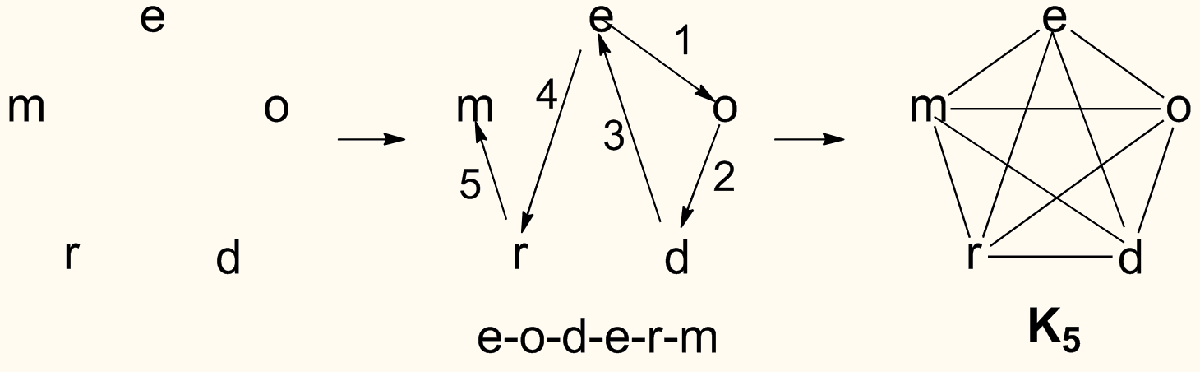
A word with a non-planar spelling net is called an eodermdrome, an ungainly name that itself illustrates the idea. The unique letters in EODERMDROME are E, O, D, R, and M. Write these down and run a pen among them, spelling out the word. You’ll find that no matter how the letters are arranged, it’s never possible to complete the task without at least two of the lines crossing:

Ross Eckler sought all the eodermdromes in Webster’s second and third editions; another example he found is SUPERSATURATES:

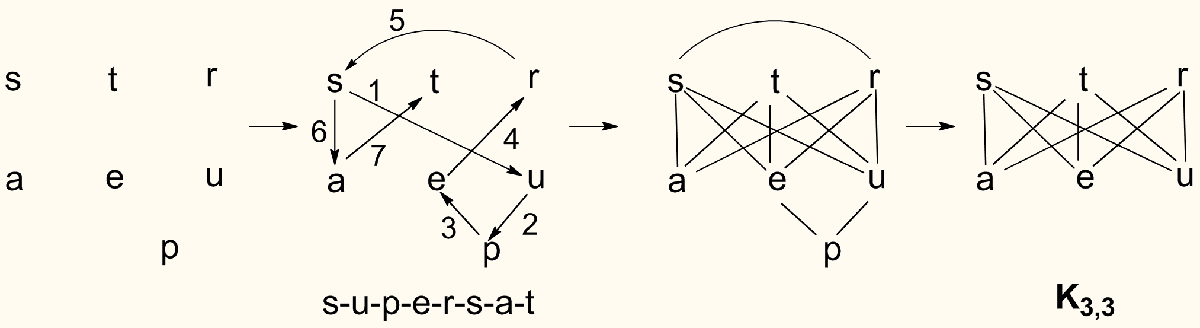
Since spelling nets are graphs, they can be studied with the tools of graph theory, the mathematical study of such networks. One result from that discipline says that a graph is non-planar if and only if it can be reduced to one of the two patterns marked K₅ and K_{(3, 3)} above. Since both EODERMDROME and SUPERSATURATES contain these forbidden graphs, both are non-planar.

A good article describing recreational eodermdrome hunting, by computer scientists Gary S. Bloom, John W. Kennedy, and Peter J. Wexler, is here. One warning: They note that, with some linguistic flexibility, the word eodermdrome can be interpreted to mean “a course on which to go to be made miserable.”