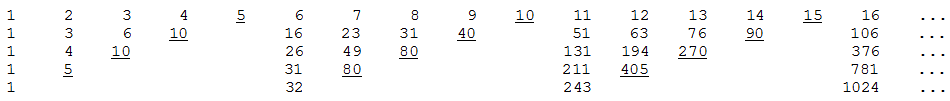
Write out the positive integers in a row and underline every fifth number. Now ignore the underlined numbers and record the partial sums of the other numbers in a second row, placing each sum directly beneath the last entry that it contains.

Now, in this second row, underline and ignore every fourth number, and record the partial sums in a third row. Keep this up and the entries in the fifth row will turn out to be the perfect fifth powers 1⁵, 2⁵, 3⁵, 4⁵, 5⁵ …

If we’d started by ignoring every fourth number in the original row, we’d have ended up with perfect fourth powers. In fact,

For every positive integer k > 1, if every kth number is ignored in row 1, every (k – 1)th number in row 2, and, in general, every (k + 1 – i)th number in row i, then the kth row of partial sums will turn out to be just the perfect kth powers 1^k, 2^k, 3^k …

This was discovered in 1951 by Alfred Moessner, a giant of recreational mathematics who published many such curiosa in Scripta Mathematica between 1932 and 1957.

(Ross Honsberger, More Mathematical Morsels, 1991.)