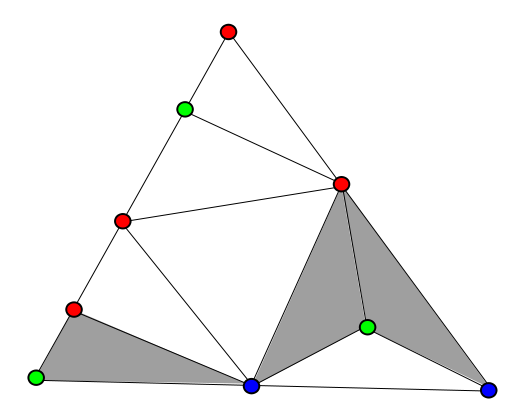
Draw a triangle and color its vertices red, green, and blue. Then divide it into as many smaller triangles as you like (the smaller triangles must meet edge to edge and vertex to vertex). Now color the vertices of these smaller triangles using the same three colors. You can do this however you like, with one proviso: The vertices that lie on a side of the large triangle must take the color of either of its ends (so, for instance, the point at the bottom center of the triangle above must be colored either green or blue, not red).

No matter how this is done, there will always exist a small triangle with vertices of three colors. In fact, there will always be an odd number of such triangles.