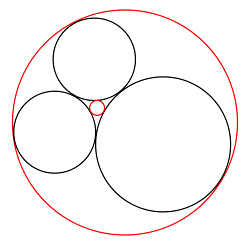
In 2014 I described Descartes’ theorem, which shows how to find a fourth circle that’s tangent to three “kissing circles.”

Descartes’ equation refers to the “curvature” of each circle: this is just the reciprocal of the radius, so a circle with radius 1/3 would have a curvature of 3. (This makes sense intuitively — a circle with a small radius “curves more” than a larger one.)

Remarkably, if the four starting circles all have integer curvature, then so will every circle we pack into the figure, each kissing the three around it. In the limit the figure becomes a fractal containing an infinite number of circles. It’s called an Apollonian gasket.

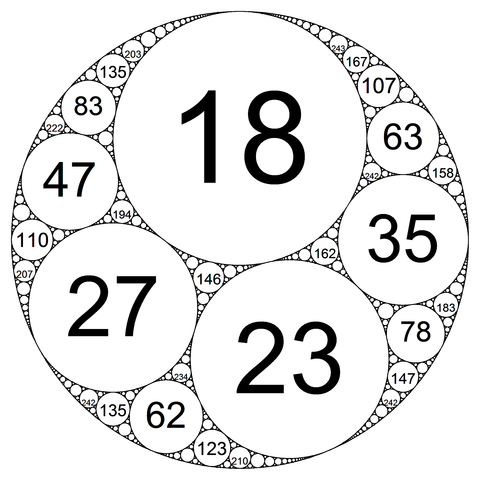
07/29/2016 UPDATE: By coincidence, the U.S. quarter, nickel, and dime make three of the four generating circles in an integral packing — see the caption accompanying the first figure on this page. (Thanks, Trevor.)