“The Pythagorean Curiosity”

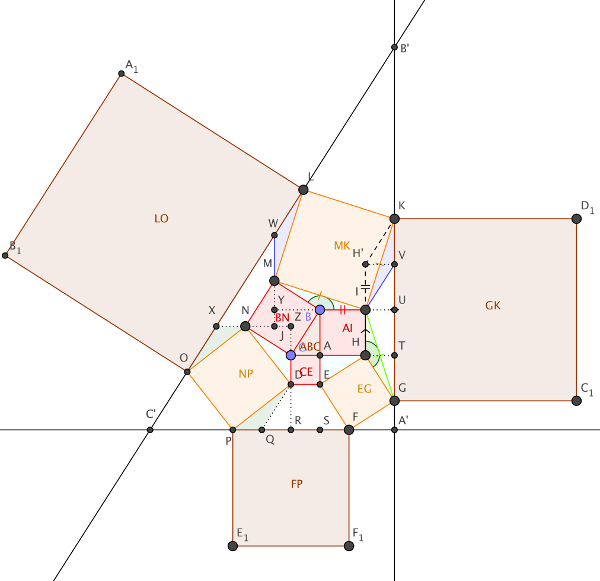
waterhouse pythagorean curiosity

Here’s the item I mentioned in Episode 99 of the podcast — New York City engineer John Waterhouse published it in July 1899. It’s not a proof of the Pythagorean theorem, as I’d thought, but rather a related curiosity. It made a splash at the time — the Proceedings of the American Society of Civil Engineers said it “interested instructors of geometry all over the country, bringing many letters of commendation to him from prominent teachers.” Listener Colin Beveridge has been immensely helpful in devising the diagram above and making sense of Waterhouse’s proof as it appears on page 252 of Elisha Scott Loomis’ 1940 book The Pythagorean Proposition. Click the diagram to enlarge it a bit further.

  1. Red squares BN = AI + CE — Pythagoras’s theorem
  2. Blue triangles AEH, CDN, BMI are all equal in area to ABC, reasoning via X and Y and base sides.
  3. Green angles GHI and IBM are equal and green triangle GHI is congruent to IBM (side angle side), so IG = IK = IM. IH′K is congruent to IHK as angle HIK = angle HIG and the adjacent sides correspond. This means G and K are the same distance from the line HH′, so GK is parallel to HI. Similarly, DE is parallel to PF and MN is parallel to LO.
  4. GK = 4HI, because TU=HI, TG = AH (HTG congruent to EAH) and UK = UG (symmetry). Similarly, PF = 4DE. Dark blue triangles IVK and LWM are equal, so WM = VK. Similarly, OX = QD (dark green triangles PQD and NXO are congruent). Also, WX=MJ and XN=NJ, so M and N are the midpoints of WJ and XJ. That makes WX=2MN, so LO = 4MN.
  5. Each of the trapezia we just looked at (HIKG, OLMN and PFED) have five times the area of ABC.
  6. The areas of orange squares MK and NP are together five times EG. This is because:
    • the square on MI is (the square on MY) + (the square on IY) = (AC2) + (2AB)2 = 4AB2 + AC2.
    • the square on ND is (the square on NZ) + (the square on DZ) = (AB2) + (2AC)2 = 4AC2 + AB2
    • the sum of these is 5(AB2 + AC2) = 5BC2, and BC = HE.
  7. A′S = A′T, so A′SAT is a square and the bisector of angle B′A′C′ passes through A. However, the bisectors of angle A′B′C′ and A′C′B′ do not pass through B and C (resp.) [Colin says Waterhouse’s reasoning for this is not immediately clear.]
  8. Square LO = square GK + square FP, as LO = 4AC, GK = 4AB and FP = 4BC.
  9. [We’re not quite sure what Waterhouse means by “etc. etc.” — perhaps that one could continue to build squares and triangles outward forever.]
| Science & Math