If you mark two points on a circle, A and B, and a third point T, then angle ATB remains constant as T moves along the segment between A and B. (If you mark a point S in the circle’s other segment then you get another constant angle, ASB, and ASB = 180 – ATB.)

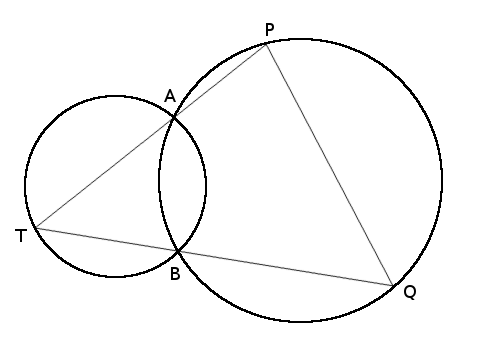
If two circles intersect at A and B and we move T as before along the segment opposite the second circle, and we extend TA and TB to P and Q on the second circle, then the length of chord PQ remains constant as T moves.

(From David Wells, The Penguin Dictionary of Curious and Interesting Geometry, 1992.)