Yes. Think of 10 straight lines in the plane, no two of which are parallel and no three of which meet at the same point. Let the lines be the bus routes and the points of intersection be the stops. At the start we can get from any one stop to any other, either directly (if they’re on the same line) or with just one change. If we remove one line, it’s still possible to get from any stop to any other with at most one change. But if we discard two lines, then one stop — the one at their intersection — will have no bus routes passing through it and thus become inaccessible to all the other stops.

(From A.M. Yaglom and I.M. Yaglom, Challenging Mathematical Problems With Elementary Solutions, 1964.)

03/04/2016 UPDATE: If multiple transfers are permitted, a simpler solution is to make a ring of the stops, with each successive pair connected by a route. Remove any one route and the graph remains connected, but remove any two it disconnects:

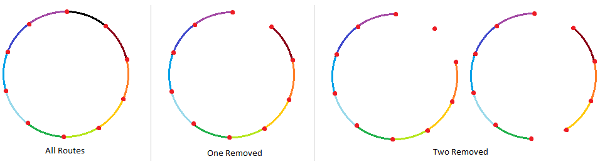
I think this may be a matter of translation. The Yagloms say that one makes a bus journey “possibly changing along the way.” Their own solution requires only one transfer.

Thanks to everyone who wrote in about this, and thanks to Herschel for the diagram.