In Pascal’s triangle, each number is the sum of the two immediately above it:

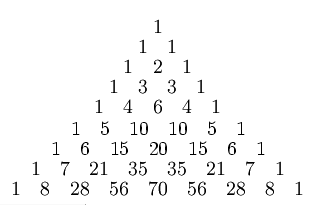
In 1972, Henry Mann and Daniel Shanks found a curious connection between the triangle and prime numbers. Stagger the triangle’s rows so that row n starts at column 2n:

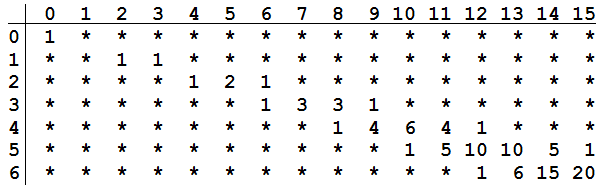
Now a column number is prime precisely when the numbers in that column are each divisible by their row number. For instance, in the diagram above, column 13 has two entries — 10, which is divisible by 5, and 6, which is divisible by 6 — so 13 is prime. The numbers in column 12 are not all evenly divisible by their row numbers, so 12 is not prime.

“It’s a nifty and surprising result,” writes James Tanton in Mathematics Galore! (2012), “but it is not a formula that allows us to find prime numbers with ease.”

(Henry B. Mann and Daniel Shanks, “A Necessary and Sufficient Condition for Primality, and Its Source,” Journal of Combinatorial Theory, Series A 13:1 [1972], 131-134.)