Three ancient problems are famously impossible to solve using a compass and straightedge alone: doubling the cube, trisecting an angle, and squaring the circle. Surprisingly, the first two of these can be solved using origami.
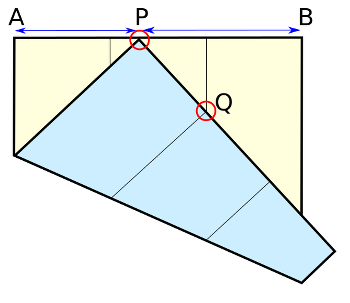
In the first, doubling the cube, we’re given the edge of one cube and asked to find the edge of a second cube whose volume is twice that of the first; if the first cube’s edge length is 1, then we’re trying to find . Begin by folding a square of paper into three equal panels (here’s how). Then draw up bottom corner P as shown above, so that it’s touching the top edge while the bottom of the first crease, Q, touches the second crease as shown. Now point P divides the top edge into two segments whose proportions are 1 and
.
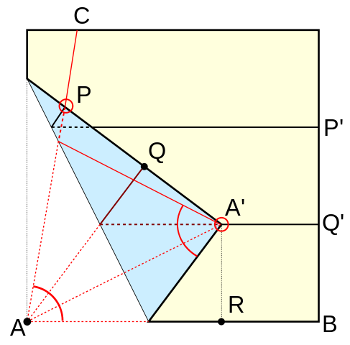
To trisect an angle, begin by marking the angle in one corner of a square (here’s it’s CAB). Make a horizontal fold, PP’, anywhere across the square. Then divide the space below this crease in half with another crease, QQ’. Fold the bottom left corner up so that corner A touches QQ’ (at A’) and P touches AC. Now A’AB is one-third of the original angle, CAB.
The first of these constructions is due to Peter Messer, the second to Hisashi Abe. Strictly speaking, each uses creases to produce a marked straightedge, which is not allowed in classical construction, but they’re pleasingly simple solutions to these vexing problems. There’s more at origami wizard Robert Lang’s website.
