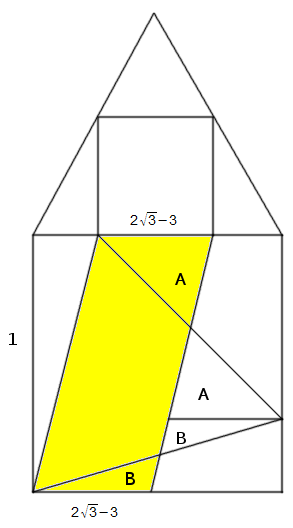
The area of the largest equilateral triangle that fits inside a unit square exactly equals the side of the largest square that fits inside a unit equilateral triangle.

This proof is due to John Conway. The largest square that fits inside a unit equilateral triangle is shown at the top; the side of the square is . The largest equilateral triangle that fits inside a unit square is one that’s canted at a 15° angle, shown at the bottom.

Now, the area of the shaded parallelogram is just its base times its height, or . And the parallelogram can be dissected into three pieces that fit precisely into the canted triangle. So the side of the square at the top equals the area of the triangle at the bottom.