In 1653, Blaise Pascal composed a triangular array in which the number in each cell is the sum of the two directly above it:

In 1915, Polish mathematician Waclaw Sierpinski described an equilateral triangle in which the central fourth is removed and the same procedure is applied to all the succeeding smaller triangles. Perplexingly, the resulting structure has zero area:

Interestingly, if the odd numbers in Pascal’s triangle are shaded, they produce an approximation to Sierpinski’s triangle:

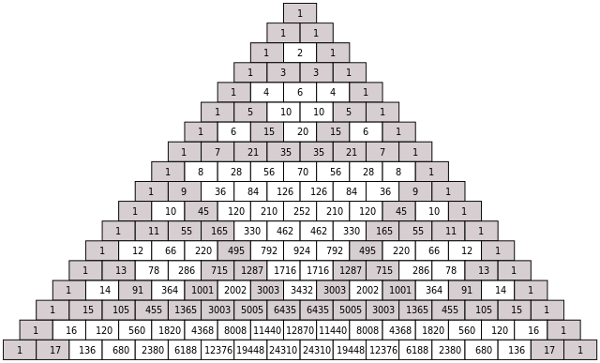
And as this triangle grows toward infinity, it becomes Sierpinski’s triangle — an arrangement of numbers that takes the shape of a geometrical object.