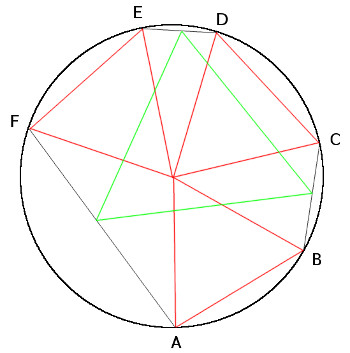
Arrange three congruent equilateral triangles so that their corners meet at a point, like the red triangles above. The arrangement doesn’t have to be symmetric; the triangles can even overlap. Now draw lines BC, DE, and FA to complete a hexagon inscribed in a circle. The midpoints of these three lines will form the vertices of an equilateral triangle.

That’s called the asymmetric propeller theorem, and it’s been known since the 1930s. But in 1979 Beverly Hills dentist and geometry enthusiast Leon Bankoff told Martin Gardner of some further discoveries. Bankoff never found time to write them up, so after the dentist’s death in 1997 Gardner published them in the College Mathematics Journal:

• The three equilateral triangles need not be congruent. Each can be of any size and the theorem still holds.
• The triangles need not meet at a point. They can meet at the corners of any equilateral triangle.
• They need not even be equilateral! If three similar triangles of any sizes meet at a point, the midpoints of the three added lines will form a triangle similar to each of the “propellers.”
• The similar triangles need not meet at a point! If they meet at the corners of a fourth triangle (of any size) that’s similar to each propeller, then the midpoints of the added lines will form a triangle similar to each propeller, provided that the vertices of the central triangle touch the corresponding corners of the propellers.

Given all this flexibility, Gardner asked, do the propellers even have to be triangles? It turns out that the answer is yes. Still, the discoveries above form a fitting tribute to Bankoff, whom Gardner called “one of the most remarkable mathematicians I have been privileged to know.”

(Martin Gardner, “The Asymmetric Propeller,” College Mathematics Journal 30:1 [January 1999], 18-22.)