Trap a circle inside a square and it can turn happily in its prison — a circle has the same breadth in any orientation.

Perhaps surprisingly, circles are not the only shapes with this property. The Reuleaux triangle has the same width in any orientation, so it can perform the same trick:

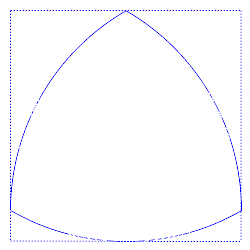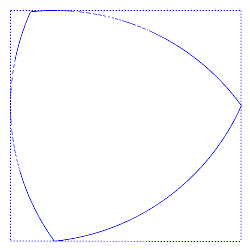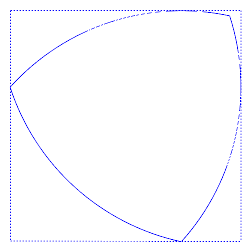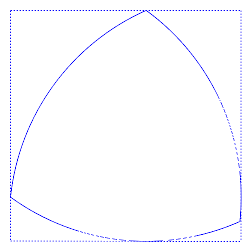
In fact any square can accommodate a whole range of “curves of constant width,” all of which have the same perimeter (πd, like the circle). Some of these are surprisingly familiar: The heptagonal British 20p and 50p coins and the 11-sided Canadian dollar coin have constant widths so that vending machines can recognize them. What other applications are possible? In the June 2014 issue of the Mathematical Intelligencer, Monash University mathematician Burkard Polster notes that a curve of constant width can produce a bit that drills square holes:

… and a unicycle with bewitching wheels:

The self-accommodating nature of such shapes permits them to take part in fascinating “dances,” such as this one among seven triangles:

This inspired Kenichi Miura to propose a water wheel whose buckets are Reuleaux triangles. As the wheel turns, each pair of adjacent buckets touch at a single point, so that no water is lost:

Here’s an immediately practical application: Retired Chinese military officer Guan Baihua has designed a bicycle with non-circular wheels of constant width — the rider’s weight rests on top of the wheels and the suspension accommodates the shifting axles:

(Burkard Polster, “Kenichi Miura’s Water Wheel, or the Dance of the Shapes of Constant Width,” Mathematical Intelligencer, June 2014.)