A “calculus problem to end all calculus problems,” by Dan Kennedy, chairman of the math department at the Baylor School, Chattanooga, Tenn., and chair of the AP Calculus Committee:

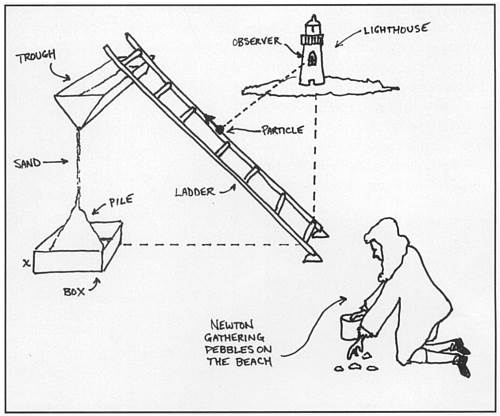
A particle starts at rest and moves with velocity along a 10-foot ladder, which leans against a trough with a triangular cross-section two feet wide and one foot high. Sand is flowing out of the trough at a constant rate of two cubic feet per hour, forming a conical pile in the middle of a sandbox which has been formed by cutting a square of side x from each corner of an 8″ by 15″ piece of cardboard and folding up the sides. An observer watches the particle from a lighthouse one mile off shore, peering through a window shaped like a rectangle surmounted by a semicircle.

(a) How fast is the tip of the shadow moving?
(b) Find the volume of the solid generated when the trough is rotated about the y-axis.
(c) Justify your answer.
(d) Using the information found in parts (a), (b), and (c) sketch the curve on a pair of coordinate axes.

From Math Horizons, Spring 1994.