A.B. Kempe’s provocatively titled How to Draw a Straight Line (1877) addresses a fundamental question. In the Elements, Euclid derives his results by drawing straight lines and circles. We can draw a circle by rotating a rigid body (such as a pair of compasses) around a fixed point. But how can we produce a straight line? “If we are to draw a straight line with a ruler, the ruler must itself have a straight edge; and how are we going to make the edge straight? We come back to our starting-point.”

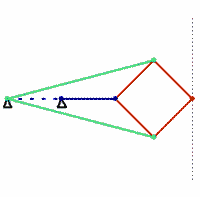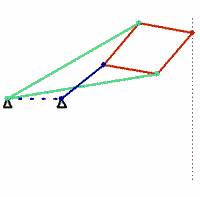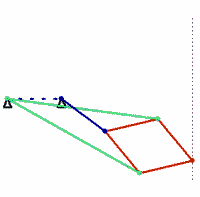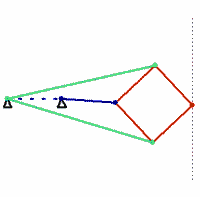
Kempe’s solution is the Peaucellier–Lipkin linkage, an ingenious mechanism that was invented in 1864 by the French army engineer Charles-Nicolas Peaucellier, forgotten, and rediscovered by a Russian student named Yom Tov Lipman Lipkin. In the figure shown here, the colors denote bars of equal length. The green and red bars form a linkage called a Peaucellier cell, and adding the blue links causes the red rhombus to flex as it moves. A pencil fixed at the outer vertex of the rhombus will draw a straight line.

James Sylvester introduced Peaucellier’s discovery to England in a lecture at the Royal Institution in January 1874, which Kempe says “excited very great interest and was the commencement of the consideration of the subject of linkages in this country.” Sylvester writes that when he showed a model of the linkage to Lord Kelvin, he “nursed it as if it had been his own child, and when a motion was made to relieve him of it, replied ‘No! I have not had nearly enough of it — it is the most beautiful thing I have ever seen in my life.'”