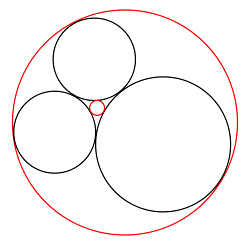
If three circles “kiss,” like the black circles above, then a fourth circle can be drawn that’s tangent to all three. In 1643 René Descartes showed that if the curvature or “bend” of a circle is defined as k = 1/r, then the radius of the fourth circle can be found by

The ± sign reflects the fact that two solutions are generally possible — the plus sign corresponds to the smaller red circle, the minus sign to the larger (circumscribing) one.

Frederick Soddy summed this up in a poem in Nature (June 20, 1936):

The Kiss Precise

For pairs of lips to kiss maybe
Involves no trigonometry.
‘Tis not so when four circles kiss
Each one the other three.
To bring this off the four must be
As three in one or one in three.
If one in three, beyond a doubt
Each gets three kisses from without.
If three in one, then is that one
Thrice kissed internally.

Four circles to the kissing come.
The smaller are the benter.
The bend is just the inverse of
The distance from the center.
Though their intrigue left Euclid dumb
There’s now no need for rule of thumb.
Since zero bend’s a dead straight line
And concave bends have minus sign,
The sum of the squares of all four bends
Is half the square of their sum.

To spy out spherical affairs
An oscular surveyor
Might find the task laborious,
The sphere is much the gayer,
And now besides the pair of pairs
A fifth sphere in the kissing shares.
Yet, signs and zero as before,
For each to kiss the other four
The square of the sum of all five bends
Is thrice the sum of their squares.

(Thanks, Sean.)