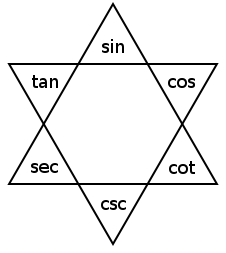
I’m not sure who came up with this — this simple diagram reflects all possible true trigonometric identities of the form x ÷ y = z or x × y = z, where x, y, and z are the basic trigonometric functions of the same angle t.

For any three neighboring functions on the perimeter of the star, the product of the ends always equals the middle (e.g., tan t × cos t = sin t) and the middle function divided by one of the end functions is equal to the other end function (e.g., sin t ÷ tan t = cos t and sin t ÷ cos t = tan t). If you memorize the diagram you can reel off a list of 18 simple relations.

I found it in Michael Stueben’s Twenty Years Before the Blackboard, 1998.