Draw any triangle and divide each leg into three equal segments. Connect each vertex to one of the trisection points on the opposite leg, as shown, and the triangle formed in the center will have 1/7 the area of the original triangle.

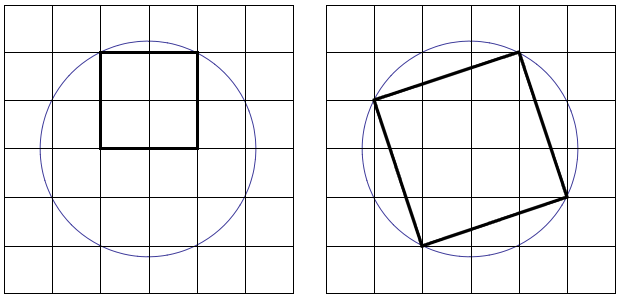
A square inscribed in a semicircle has 2/5 the area of a square inscribed in a circle of the same radius.

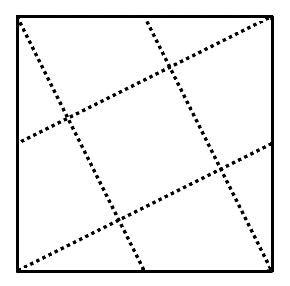
Draw a square and connect each vertex to the midpoint of an opposite side, as shown. The square formed in the center will have 1/5 the area of the original square.

A “proof without words”:

Trisect each side of a triangle and join each vertex to the opposite trisection points. Then write a hexagram in the hexagon in the center. The area of the hexagram is 7/100 the area of the original triangle.