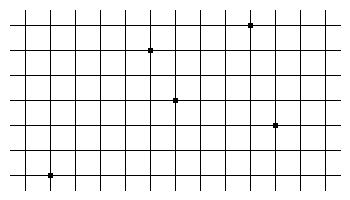
Plot five points at random at the intersections of a coordinate grid. Between each pair of points a line segment can be drawn. Prove that the midpoint of at least one of these segments occurs at an intersection of grid lines.
|
SelectClick for Answer |
The coordinates of each point can be categorized by their parity — for example, (1, 1) is odd-odd and (4, 17) is even-odd. The midpoint of a line segment between two points will occur at a lattice point only if the two endpoints fall into the same category; for example, the two points above won’t produce such a midpoint, but (6, 8) and (14, 2) will because both are even-even.
There are only four possible categories: even-even, odd-odd, even-odd, and odd-even. And because we are plotting five points, at least two points must fall into the same category. The midpoint between these two points will occur at a lattice point.
From L.C. Larsen, Problem Solving Through Problems, 1983.
|

