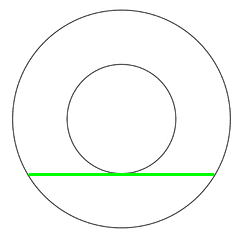
A carnival worker is asked to paint the deck of a carousel. Because the center of the carousel is occupied by machinery, he can’t measure its diameter or even its radius. The best he can do is to take the measurement shown in green, which is 42 feet.
He’s explaining this apologetically when his supervisor stops him. “That’s all the information we need,” he says. “That’s enough to tell us how much paint to buy.”
How did they go about it?
|
SelectClick for Answer |
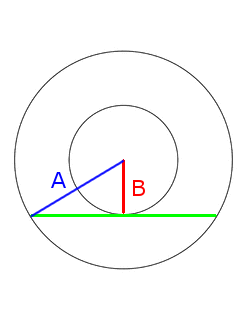
The area of the deck is the area of the large circle minus the small circle. That’s πA2 – πB2, or π(A2 – B2).
We don’t know A or B, but we do know the length of the green line. That’s 42. So the Pythagorean theorem can tell us that B2 + 212 = A2, and hence that 212 = A2 – B2. Happily, we can plug this directly into the equation above and get our answer: The area of the deck is 212π, or 441π square feet — regardless of the size of the carousel!
Remarkably, this is true — so long as the green chord stays locked in position between them, the two circles can assume any size and the difference in their areas will remain constant. A similar principle holds in three dimensions.
In The Universal Book of Mathematics, David Darling writes, “An even more amazing fact is that if you slide a chord of fixed length around any convex shape C so that the chord’s midpoint traces out another figure D, the area between C and D doesn’t depend on what shape you started with.”
(Thanks, Dave.)
|


