Choose a prime number p, draw a p×p array, and fill it with integers like so:

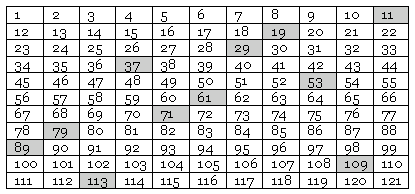
Now: Can we always find p cells that contain prime numbers such that no two occupy the same row or column? (This is somewhat like arranging rooks on a chessboard so that every rank and file is occupied but no rook attacks another.)

The example above shows one solution for p=11. Does a solution exist for every prime number? No one knows.