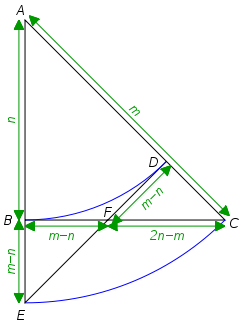
Caltech number theorist Tom Apostol devised this elegant proof of the irrationality of 
Suppose the number is rational. Then there must be an isosceles right triangle with minimum integer sides (here, triangle ABC with sides n and hypotenuse m).
By drawing two arcs as shown, we can immediately establish triangle FDC — a smaller isosceles right triangle with integer sides.
This leads to an infinite descent. Hence n and m can’t both be integers, and