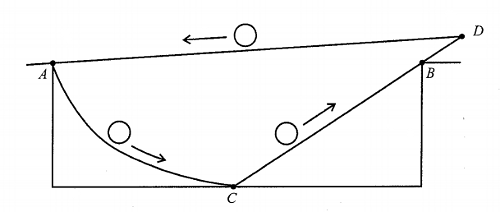
Eric Chandler offered this perpetual-motion scheme for Edward Barbeau’s “Fallacies, Flaws and Flimflam” column in the College Mathematical Journal. Points A and B are at the same height, and C is halfway between them. The ramp AC is a segment of a cycloid, a curve designed to produce the fastest descent under gravity.

A ball released at A rolls down the ramp AC to C covering a greater distance in a shorter time than it would have had it rolled down BC to C. The relation Velocity = Distance/Time thus implies that the ball arrives at C with greater velocity than it would have had it rolled down BC. This added velocity enables the ball to roll from C up to and past B to a point D a little farther along. It then returns to A along the inclined ramp DA to repeat the cycle endlessly.

Where is the error?