In Scripta Mathematica, March 1955, Pedro A. Pisa offers an unkillably valid equation:

123789 + 561945 + 642864 = 242868 + 323787 + 761943

Hack away at its terms, from either end, and it remains true:

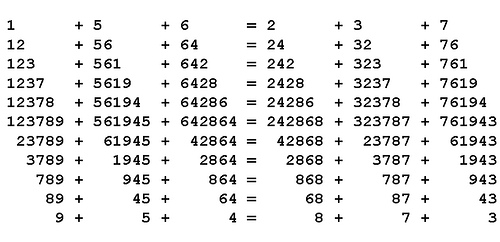
Stab it in the heart, removing the two center digits from each term, and it still balances:

1289 + 5645 + 6464 = 2468 + 3287 + 7643

Do this again and it still balances:

19 + 55 + 64 = 28 + 37 + 73

Most amazing: You can square every term above, in every equation, and they’ll all remain true.

12/03/2016 UPDATE: Reader Jean-Claude Georges discovered that the equalities remain valid when any combination of digits is removed consistently across terms. For example, starting from

123789 + 561945 + 642864 == 242868 + 323787 + 761943,

removing the 1st, 3rd and 5th digit from each number:

x2x7x9 + x6x9x5 + x4x8x4 == x4x8x8 + x2x7x7 + x6x9x3

gives

279 + 695 + 484 = 488 + 277 + 693 (= 1458)

and squaring each term gives

279² + 695² + 484² = 488² + 277² + 693² (=795122).

Amazingly, the same is true for any combination — for example, the equations remain valid when the 1st, 2nd, 4th, and 6th digits of each term are removed. (Thanks, Jean-Claude.)